
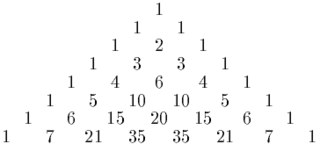
In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers n ≥ k ≥ 0 and is written It is the coefficient of the xk term in the polynomial expansion of the binomial power (1 + x)n; this coefficient can be computed by the multiplicative formula
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. For example, for n = 4,
In mathematics, the Bernoulli numbersBn are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of m-th powers of the first n positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function.
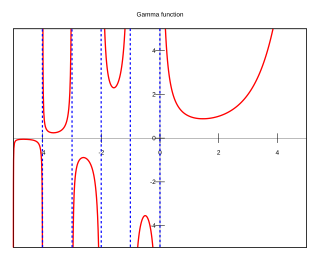
In mathematics, the gamma function is one commonly used extension of the factorial function to complex numbers. The gamma function is defined for all complex numbers except the non-positive integers. For every positive integer n,

In probability theory and statistics, the negative binomial distribution is a discrete probability distribution that models the number of failures in a sequence of independent and identically distributed Bernoulli trials before a specified (non-random) number of successes occurs. For example, we can define rolling a 6 on a dice as a success, and rolling any other number as a failure, and ask how many failure rolls will occur before we see the third success. In such a case, the probability distribution of the number of failures that appear will be a negative binomial distribution.
In mathematics, Stirling numbers arise in a variety of analytic and combinatorial problems. They are named after James Stirling, who introduced them in a purely algebraic setting in his book Methodus differentialis (1730). They were rediscovered and given a combinatorial meaning by Masanobu Saka in 1782.

In numerical analysis, the Lagrange interpolating polynomial is the unique polynomial of lowest degree that interpolates a given set of data.
In mathematics, the falling factorial is defined as the polynomial
In mathematics, summation is the addition of a sequence of numbers, called addends or summands; the result is their sum or total. Beside numbers, other types of values can be summed as well: functions, vectors, matrices, polynomials and, in general, elements of any type of mathematical objects on which an operation denoted "+" is defined.
The Touchard polynomials, studied by Jacques Touchard, also called the exponential polynomials or Bell polynomials, comprise a polynomial sequence of binomial type defined by
In mathematics, the double factorial of a number n, denoted by n‼, is the product of all the positive integers up to n that have the same parity as n. That is,
In mathematics, the binomial series is a generalization of the polynomial that comes from a binomial formula expression like for a nonnegative integer . Specifically, the binomial series is the MacLaurin series for the function , where and . Explicitly,

In mathematics, the Laguerre polynomials, named after Edmond Laguerre (1834–1886), are nontrivial solutions of Laguerre's differential equation:
In mathematics, the Gaussian binomial coefficients are q-analogs of the binomial coefficients. The Gaussian binomial coefficient, written as or , is a polynomial in q with integer coefficients, whose value when q is set to a prime power counts the number of subspaces of dimension k in a vector space of dimension n over , a finite field with q elements; i.e. it is the number of points in the finite Grassmannian .

In mathematics, the Stieltjes constants are the numbers that occur in the Laurent series expansion of the Riemann zeta function:
In mathematics the nth central binomial coefficient is the particular binomial coefficient
In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the Stirling numbers of the first kind count permutations according to their number of cycles.
In mathematics, Faulhaber's formula, named after the early 17th century mathematician Johann Faulhaber, expresses the sum of the p-th powers of the first n positive integers
In mathematics, the Schuette–Nesbitt formula is a generalization of the inclusion–exclusion principle. It is named after Donald R. Schuette and Cecil J. Nesbitt.

Anatoly Alexeyevich Karatsuba was a Russian mathematician working in the field of analytic number theory, p-adic numbers and Dirichlet series.



































