Q-analog

Last updated December 28, 2024 • 4 min readFrom Wikipedia, The Free Encyclopedia

In mathematics, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as $q \to 1$ . Typically, mathematicians are interested in q-analogs that arise naturally, rather than in arbitrarily contriving q-analogs of known results. The earliest q-analog studied in detail is the basic hypergeometric series, which was introduced in the 19th century.^[1]

q-analogs are most frequently studied in the mathematical fields of combinatorics and special functions. In these settings, the limit $q \to 1$ is often formal, as $q$ is often discrete-valued (for example, it may represent a prime power). q-analogs find applications in a number of areas, including the study of fractals and multi-fractal measures, and expressions for the entropy of chaotic dynamical systems. The relationship to fractals and dynamical systems results from the fact that many fractal patterns have the symmetries of Fuchsian groups in general (see, for example Indra's pearls and the Apollonian gasket) and the modular group in particular. The connection passes through hyperbolic geometry and ergodic theory, where the elliptic integrals and modular forms play a prominent role; the q-series themselves are closely related to elliptic integrals.

q-analogs also appear in the study of quantum groups and in q-deformed superalgebras. The connection here is similar, in that much of string theory is set in the language of Riemann surfaces, resulting in connections to elliptic curves, which in turn relate to q-series.

"Classical" q-theory

Classical q-theory begins with the q-analogs of the nonnegative integers.^[2] The equality

\lim _{q\rightarrow 1}{\frac {1-q^{n}}{1-q}}=n

suggests that we define the q-analog of n, also known as the q-bracket or q-number of n, to be

[n]_{q}={\frac {1-q^{n}}{1-q}}=1+q+q^{2}+\ldots +q^{n-1}.

By itself, the choice of this particular q-analog among the many possible options is unmotivated. However, it appears naturally in several contexts. For example, having decided to use [n]_q as the q-analog of n, one may define the q-analog of the factorial, known as the q-factorial, by

{\begin{aligned}\,[n]_{q}!&=[1]_{q}\cdot [2]_{q}\cdots [n-1]_{q}\cdot [n]_{q}\\[6pt]&={\frac {1-q}{1-q}}\cdot {\frac {1-q^{2}}{1-q}}\cdots {\frac {1-q^{n-1}}{1-q}}\cdot {\frac {1-q^{n}}{1-q}}\\[6pt]&=1\cdot (1+q)\cdots (1+q+\cdots +q^{n-2})\cdot (1+q+\cdots +q^{n-1}).\end{aligned}}

This q-analog appears naturally in several contexts. Notably, while n! counts the number of permutations of length n, [n]_q! counts permutations while keeping track of the number of inversions. That is, if inv(w) denotes the number of inversions of the permutation w and S_n denotes the set of permutations of length n, we have

\sum _{w\in S_{n}}q^{{\text{inv}}(w)}=[n]_{q}!.

In particular, one recovers the usual factorial by taking the limit as $q\rightarrow 1$ .

The q-factorial also has a concise definition in terms of the q-Pochhammer symbol, a basic building-block of all q-theories:

[n]_{q}!={\frac {(q;q)_{n}}{(1-q)^{n}}}.

From the q-factorials, one can move on to define the q-binomial coefficients, also known as Gaussian coefficients, Gaussian polynomials, or Gaussian binomial coefficients:

{\binom {n}{k}}_{q}={\frac {[n]_{q}!}{[n-k]_{q}![k]_{q}!}}.

The q-exponential is defined as:

e_{q}(x)=\sum _{n=0}^{\infty }{\frac {x^{n}}{[n]_{q}!}}.

q-trigonometric functions, along with a q-Fourier transform, have been defined in this context.

Combinatorial q-analogs

The Gaussian coefficients count subspaces of a finite vector space. Let q be the number of elements in a finite field. (The number q is then a power of a prime number, q = p^e, so using the letter q is especially appropriate.) Then the number of k-dimensional subspaces of the n-dimensional vector space over the q-element field equals

{\binom {n}{k}}_{q}.

Letting q approach 1, we get the binomial coefficient

{\binom {n}{k}},

or in other words, the number of k-element subsets of an n-element set.

Thus, one can regard a finite vector space as a q-generalization of a set, and the subspaces as the q-generalization of the subsets of the set. As another example, the number of flags is $[n]_{q}!$ as the order in which we build the flag matters, and after taking the limit we get $n!$ . This has been a fruitful point of view in finding interesting new theorems. For example, there are q-analogs of Sperner's theorem ^[3] and Ramsey theory. ^{[ citation needed ]}

Cyclic sieving

Let q = (e^{2 $π$ i/n})^d be the d-th power of a primitive n-th root of unity. Let C be a cyclic group of order n generated by an element c. Let X be the set of k-element subsets of the n-element set {1, 2, ..., n}. The group C has a canonical action on X given by sending c to the cyclic permutation (1, 2, ..., n). Then the number of fixed points of c^d on X is equal to

{\binom {n}{k}}_{q}.

q → 1

Conversely, by letting q vary and seeing q-analogs as deformations, one can consider the combinatorial case of q = 1 as a limit of q-analogs as q → 1 (often one cannot simply let q = 1 in the formulae, hence the need to take a limit).

This can be formalized in the field with one element, which recovers combinatorics as linear algebra over the field with one element: for example, Weyl groups are simple algebraic groups over the field with one element.

Applications in the physical sciences

q-analogs are often found in exact solutions of many-body problems.^{[ citation needed ]} In such cases, the $q \to 1$ limit usually corresponds to relatively simple dynamics, e.g., without nonlinear interactions, while $q < 1$ gives insight into the complex nonlinear regime with feedbacks.

An example from atomic physics is the model of molecular condensate creation from an ultra cold fermionic atomic gas during a sweep of an external magnetic field through the Feshbach resonance.^[4] This process is described by a model with a q-deformed version of the SU(2) algebra of operators, and its solution is described by q-deformed exponential and binomial distributions.

Related Research Articles

In mathematics, the binomial coefficients are the positive integers that occur as coefficients in the binomial theorem. Commonly, a binomial coefficient is indexed by a pair of integers $n \geq k \geq 0$ and is written $It is the coefficient of the x k term in the polynomial expansion of the binomial power (1 + x) n; this coefficient can be computed by the multiplicative formula$

In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, the power ⁠ $⁠$ expands into a polynomial with terms of the form ⁠ $⁠$ , where the exponents ⁠ $⁠$ and ⁠ $⁠$ are nonnegative integers satisfying ⁠ $⁠$ and the coefficient ⁠ $⁠$ of each term is a specific positive integer depending on ⁠ $⁠$ and ⁠ $⁠$ . For example, for ⁠ $⁠$ ,

In mathematics, a combination is a selection of items from a set that has distinct members, such that the order of selection does not matter. For example, given three fruits, say an apple, an orange and a pear, there are three combinations of two that can be drawn from this set: an apple and a pear; an apple and an orange; or a pear and an orange. More formally, a k-combination of a set S is a subset of k distinct elements of S. So, two combinations are identical if and only if each combination has the same members. If the set has n elements, the number of k-combinations, denoted by $or, is equal to the binomial coefficient$

In mathematics, the factorial of a non-negative integer $,$ denoted by $,$ is the product of all positive integers less than or equal to $.$ The factorial of also equals the product of $with the next smaller factorial: For example, The value of 0! is 1, according to the convention for an empty product.$

A finite difference is a mathematical expression of the form $f (x + b) - f (x + a)$ . If a finite difference is divided by $b - a$ , one gets a difference quotient. The approximation of derivatives by finite differences plays a central role in finite difference methods for the numerical solution of differential equations, especially boundary value problems.

In mathematics, a recurrence relation is an equation according to which the $th term of a sequence of numbers is equal to some combination of the previous terms. Often, only previous terms of the sequence appear in the equation, for a parameter that is independent of; this number is called the order of the relation. If the values of the first numbers in the sequence have been given, the rest of the sequence can be calculated by repeatedly applying the equation.$

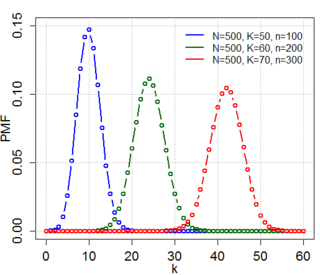
<span class="mw-page-title-main">Hypergeometric distribution</span> Discrete probability distribution

In probability theory and statistics, the hypergeometric distribution is a discrete probability distribution that describes the probability of $successes in draws, without replacement, from a finite population of size that contains exactly objects with that feature, wherein each draw is either a success or a failure. In contrast, the binomial distribution describes the probability of successes in draws with replacement.$

In mathematics, the falling factorial is defined as the polynomial

In mathematics, the Erdős–Ko–Rado theorem limits the number of sets in a family of sets for which every two sets have at least one element in common. Paul Erdős, Chao Ko, and Richard Rado proved the theorem in 1938, but did not publish it until 1961. It is part of the field of combinatorics, and one of the central results of extremal set theory.

In mathematics, a multiset is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the multiplicity of that element in the multiset. As a consequence, an infinite number of multisets exist that contain only elements $a$ and $b$ , but vary in the multiplicities of their elements:

In mathematics, the double factorial of a number $n$ , denoted by $n ‼$ , is the product of all the positive integers up to $n$ that have the same parity as $n$ . That is,

In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.

Sperner's theorem, in discrete mathematics, describes the largest possible families of finite sets none of which contain any other sets in the family. It is one of the central results in extremal set theory. It is named after Emanuel Sperner, who published it in 1928.

In probability theory, the factorial moment is a mathematical quantity defined as the expectation or average of the falling factorial of a random variable. Factorial moments are useful for studying non-negative integer-valued random variables, and arise in the use of probability-generating functions to derive the moments of discrete random variables.

In combinatorics, Vandermonde's identity is the following identity for binomial coefficients:

In mathematics, the Gaussian binomial coefficients are q-analogs of the binomial coefficients. The Gaussian binomial coefficient, written as $or, is a polynomial in q with integer coefficients, whose value when q is set to a prime power counts the number of subspaces of dimension k in a vector space of dimension n over, a finite field with q elements; i.e. it is the number of points in the finite Grassmannian .$

In mathematics, especially in combinatorics, Stirling numbers of the first kind arise in the study of permutations. In particular, the unsigned Stirling numbers of the first kind count permutations according to their number of cycles.

In combinatorics, the twelvefold way is a systematic classification of 12 related enumerative problems concerning two finite sets, which include the classical problems of counting permutations, combinations, multisets, and partitions either of a set or of a number. The idea of the classification is credited to Gian-Carlo Rota, and the name was suggested by Joel Spencer.

In mathematics, in the field of combinatorics, the q-Vandermonde identity is a q-analogue of the Chu–Vandermonde identity. Using standard notation for q-binomial coefficients, the identity states that

In the mathematical field of combinatorics, the q-Pochhammer symbol, also called the q-shifted factorial, is the product $with It is a q -analog of the Pochhammer symbol, in the sense that The q -Pochhammer symbol is a major building block in the construction of q -analogs; for instance, in the theory of basic hypergeometric series, it plays the role that the ordinary Pochhammer symbol plays in the theory of generalized hypergeometric series.$

References

Andrews, G. E., Askey, R. A. & Roy, R. (1999), Special Functions, Cambridge University Press, Cambridge.
Gasper, G. & Rahman, M. (2004), Basic Hypergeometric Series, Cambridge University Press, ISBN 0521833574.
Ismail, M. E. H. (2005), Classical and Quantum Orthogonal Polynomials in One Variable, Cambridge University Press.
Koekoek, R. & Swarttouw, R. F. (1998), The Askey-scheme of hypergeometric orthogonal polynomials and its q-analogue, 98-17, Delft University of Technology, Faculty of Information Technology and Systems, Department of Technical Mathematics and Informatics.

↑ Exton, H. (1983), q-Hypergeometric Functions and Applications, New York: Halstead Press, Chichester: Ellis Horwood, 1983, ISBN 0853124914 , ISBN 0470274530 , ISBN 978-0470274538
↑ Ernst, Thomas (2003). "A Method for q-calculus" (PDF). Journal of Nonlinear Mathematical Physics. 10 (4): 487–525. Bibcode:2003JNMP...10..487E. doi: 10.2991/jnmp.2003.10.4.5 . Archived (PDF) from the original on 2012-03-28. Retrieved 2011-07-27.
↑ Rota, Gian-Carlo; Harper, L. H. (1971), "Matching theory, an introduction", Advances in Probability and Related Topics, Vol. 1, New York: Dekker, pp. 169–215, MR 0282855 .
↑ C. Sun; N. A. Sinitsyn (2016). "Landau-Zener extension of the Tavis-Cummings model: Structure of the solution". Phys. Rev. A . 94 (3): 033808. arXiv: 1606.08430 . Bibcode:2016PhRvA..94c3808S. doi:10.1103/PhysRevA.94.033808.

External links

"Umbral calculus", Encyclopedia of Mathematics , EMS Press, 2001 [1994]
q-analog from MathWorld
q-bracket from MathWorld
q-factorial from MathWorld
q-binomial coefficient from MathWorld

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Exton, H. (1983), q-Hypergeometric Functions and Applications, New York: Halstead Press, Chichester: Ellis Horwood, 1983, ISBN 0853124914 , ISBN 0470274530 , ISBN 978-0470274538

[Ernst2003-2] Ernst, Thomas (2003). "A Method for q-calculus" (PDF). Journal of Nonlinear Mathematical Physics. 10 (4): 487–525. Bibcode:2003JNMP...10..487E. doi: 10.2991/jnmp.2003.10.4.5 . Archived (PDF) from the original on 2012-03-28. Retrieved 2011-07-27.

[3] Rota, Gian-Carlo; Harper, L. H. (1971), "Matching theory, an introduction", Advances in Probability and Related Topics, Vol. 1, New York: Dekker, pp. 169–215, MR 0282855 .

[sun-16pra2-4] C. Sun; N. A. Sinitsyn (2016). "Landau-Zener extension of the Tavis-Cummings model: Structure of the solution". Phys. Rev. A . 94 (3): 033808. arXiv: 1606.08430 . Bibcode:2016PhRvA..94c3808S. doi:10.1103/PhysRevA.94.033808.

[1]

[2]

[3]

[4]