Related Research Articles
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many applications ranging from logic to statistical physics and from evolutionary biology to computer science.
Christopher Francis Freiling is a mathematician responsible for Freiling's axiom of symmetry in set theory. He has also made significant contributions to coding theory, in the process establishing connections between that field and matroid theory.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is sometimes called a planar matroid ; these are exactly the graphic matroids formed from planar graphs.

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act.
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.
The carpenter's rule problem is a discrete geometry problem, which can be stated in the following manner: Can a simple planar polygon be moved continuously to a position where all its vertices are in convex position, so that the edge lengths and simplicity are preserved along the way? A closely related problem is to show that any non-self-crossing polygonal chain can be straightened, again by a continuous transformation that preserves edge distances and avoids crossings.

In geometry, a flexible polyhedron is a polyhedral surface without any boundary edges, whose shape can be continuously changed while keeping the shapes of all of its faces unchanged. The Cauchy rigidity theorem shows that in dimension 3 such a polyhedron cannot be convex.
Robert Connelly is a mathematician specializing in discrete geometry and rigidity theory. Connelly received his Ph.D. from University of Michigan in 1969. He is currently a professor at Cornell University.

In Euclidean plane geometry, a pseudotriangle (pseudo-triangle) is the simply connected subset of the plane that lies between any three mutually tangent convex sets. A pseudotriangulation (pseudo-triangulations) is a partition of a region of the plane into pseudotriangles, and a pointed pseudotriangulation is a pseudotriangulation in which at each vertex the incident edges span an angle of less than π.
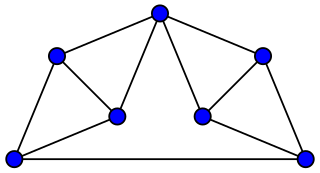
In graph theory, the Laman graphs are a family of sparse graphs describing the minimally rigid systems of rods and joints in the plane. Formally, a Laman graph is a graph on n vertices such that, for all k, every k-vertex subgraph has at most 2k − 3 edges, and such that the whole graph has exactly 2n − 3 edges. Laman graphs are named after Gerard Laman, of the University of Amsterdam, who in 1970 used them to characterize rigid planar structures. This characterization, however, had already been discovered in 1927 by Hilda Geiringer.
Discrete Morse theory is a combinatorial adaptation of Morse theory developed by Robin Forman. The theory has various practical applications in diverse fields of applied mathematics and computer science, such as configuration spaces, homology computation, denoising, mesh compression, and topological data analysis.

Jessen's icosahedron, sometimes called Jessen's orthogonal icosahedron, is a non-convex polyhedron with the same numbers of vertices, edges, and faces as the regular icosahedron. It is named for Børge Jessen, who studied it in 1967. In 1971, a family of nonconvex polyhedra including this shape was independently discovered and studied by Adrien Douady under the name six-beakedshaddock; later authors have applied variants of this name more specifically to Jessen's icosahedron.

In discrete geometry and mechanics, structural rigidity is a combinatorial theory for predicting the flexibility of ensembles formed by rigid bodies connected by flexible linkages or hinges.
Jacob Eli Goodman was an American geometer who spent most of his career at the City College of New York, where he was professor emeritus.
In the mathematics of structural rigidity, a rigidity matroid is a matroid that describes the number of degrees of freedom of an undirected graph with rigid edges of fixed lengths, embedded into Euclidean space. In a rigidity matroid for a graph with n vertices in d-dimensional space, a set of edges that defines a subgraph with k degrees of freedom has matroid rank dn − k. A set of edges is independent if and only if, for every edge in the set, removing the edge would increase the number of degrees of freedom of the remaining subgraph.
In the mathematical theory of matroids, a matroid representation is a family of vectors whose linear independence relation is the same as that of a given matroid. Matroid representations are analogous to group representations; both types of representation provide abstract algebraic structures with concrete descriptions in terms of linear algebra.
In matroid theory, a mathematical discipline, the girth of a matroid is the size of its smallest circuit or dependent set. The cogirth of a matroid is the girth of its dual matroid. Matroid girth generalizes the notion of the shortest cycle in a graph, the edge connectivity of a graph, Hall sets in bipartite graphs, even sets in families of sets, and general position of point sets. It is hard to compute, but fixed-parameter tractable for linear matroids when parameterized both by the matroid rank and the field size of a linear representation.
Brigitte Irma Servatius is a mathematician specializing in matroids and structural rigidity. She is a professor of mathematics at Worcester Polytechnic Institute, and has been the editor-in-chief of the Pi Mu Epsilon Journal since 1999.
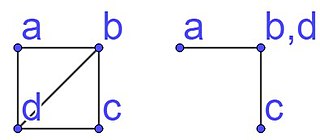
In discrete geometry, geometric rigidity is a theory for determining if a geometric constraint system (GCS) has finitely many -dimensional solutions, or frameworks, in some metric space. A framework of a GCS is rigid in -dimensions, for a given if it is an isolated solution of the GCS, factoring out the set of trivial motions, or isometric group, of the metric space, e.g. translations and rotations in Euclidean space. In other words, a rigid framework of a GCS has no nearby framework of the GCS that is reachable via a non-trivial continuous motion of that preserves the constraints of the GCS. Structural rigidity is another theory of rigidity that concerns generic frameworks, i.e., frameworks whose rigidity properties are representative of all frameworks with the same constraint graph. Results in geometric rigidity apply to all frameworks; in particular, to non-generic frameworks.
References
- ↑ Faculty, York University Department of Mathematics and Statistics, retrieved 2015-11-21.
- 1 2 Curriculum vitae: Walter John Whiteley (PDF), April 2001, retrieved 2015-11-21.
- 1 2 3 2009 Adrien Pouliot Award (PDF), Canadian Mathematical Society , retrieved 2015-11-21.
- ↑ Walter Whiteley at the Mathematics Genealogy Project
- ↑ Workshop on Making Models: Stimulating Research In Rigidity Theory And Spatial-Visual Reasoning, Held at the Fields Institute, August 5–9, 2014, retrieved 2015-11-21.