
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Accelerations are vector quantities. The orientation of an object's acceleration is given by the orientation of the net force acting on that object. The magnitude of an object's acceleration, as described by Newton's Second Law, is the combined effect of two causes:
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such models in the 19th century.
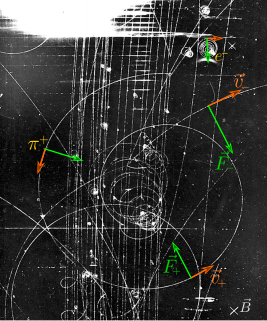
In physics the Lorentz force is the combination of electric and magnetic force on a point charge due to electromagnetic fields. A particle of charge q moving with a velocity v in an electric field E and a magnetic field B experiences a force of

In Newtonian mechanics, linear momentum, translational momentum, or simply momentum is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If m is an object's mass and v is its velocity, then the object's momentum is:
In SI units, momentum is measured in kilogram meters per second (kg⋅m/s).
In mechanics, the virial theorem provides a general equation that relates the average over time of the total kinetic energy of a stable system of discrete particles, bound by potential forces, with that of the total potential energy of the system. Mathematically, the theorem states

In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behaviour of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system. The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describing the motion of the dynamics.
Kinematics is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies without considering the forces that cause them to move. Kinematics, as a field of study, is often referred to as the "geometry of motion" and is occasionally seen as a branch of mathematics. A kinematics problem begins by describing the geometry of the system and declaring the initial conditions of any known values of position, velocity and/or acceleration of points within the system. Then, using arguments from geometry, the position, velocity and acceleration of any unknown parts of the system can be determined. The study of how forces act on bodies falls within kinetics, not kinematics. For further details, see analytical dynamics.
In physics, angular velocity, also known as angular frequency vector, is a vector measure of rotation rate, that refers to how fast an object rotates or revolves relative to another point, i.e. how fast the angular position or orientation of an object changes with time.
In physics, angular acceleration refers to the time rate of change of angular velocity. As there are two types of angular velocity, namely spin angular velocity and orbital angular velocity, there are naturally also two types of angular acceleration, called spin angular acceleration and orbital angular acceleration respectively. Spin angular acceleration refers to the angular acceleration of a rigid body about its centre of rotation, and orbital angular acceleration refers to the angular acceleration of a point particle about a fixed origin.

In physics, work is the energy transferred to or from an object via the application of force along a displacement. In its simplest form, it is often represented as the product of force and displacement. A force is said to do positive work if it has a component in the direction of the displacement of the point of application. A force does negative work if it has a component opposite to the direction of the displacement at the point of application of the force.
In physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective (macroscopic) variables changing only slowly in comparison to the other (microscopic) variables of the system. The fast (microscopic) variables are responsible for the stochastic nature of the Langevin equation. One application is to Brownian motion, calculating the statistics of the random motion of a small particle in a fluid due to collisions with the surrounding molecules in thermal motion.
In analytical mechanics, the term generalized coordinates refers to the parameters that describe the configuration of the system relative to some reference configuration. These parameters must uniquely define the configuration of the system relative to the reference configuration. This is done assuming that this can be done with a single chart. The generalized velocities are the time derivatives of the generalized coordinates of the system.

In continuum mechanics and thermodynamics, a control volume is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fictitious volume fixed in space or moving with constant flow velocity through which the continuum flows. The surface enclosing the control volume is referred to as the control surface.
In a compressible sound transmission medium - mainly air - air particles get an accelerated motion: the particle acceleration or sound acceleration with the symbol a in metre/second2. In acoustics or physics, acceleration is defined as the rate of change of velocity. It is thus a vector quantity with dimension length/time2. In SI units, this is m/s2.
'Linear motion' is also called rectilinear motion is a one-dimensional motion along a straight line, and can therefore be described mathematically using only one spatial dimension. The linear motion can be of two types: uniform linear motion with constant velocity or zero acceleration; non uniform linear motion with variable velocity or non-zero acceleration. The motion of a particle along a line can be described by its position , which varies with (time). An example of linear motion is an athlete running 100m along a straight track.
In classical mechanics, Euler's laws of motion are equations of motion which extend Newton's laws of motion for point particle to rigid body motion. They were formulated by Leonhard Euler about 50 years after Isaac Newton formulated his laws.

Lagrangian mechanics is a reformulation of classical mechanics, introduced by the Italian-French mathematician and astronomer Joseph-Louis Lagrange in 1788.
In classical mechanics, the central-force problem is to determine the motion of a particle in a single central potential field. A central force is a force that points from the particle directly towards a fixed point in space, the center, and whose magnitude only depends on the distance of the object to the center. In many important cases, the problem can be solved analytically, i.e., in terms of well-studied functions such as trigonometric functions.

In mechanics, a variable-mass system is a collection of matter whose mass varies with time. It can be confusing to try to apply Newton's second law of motion directly to such a system. Instead, the time dependence of the mass m can be calculated by rearranging Newton's second law and adding a term to account for the momentum carried by mass entering or leaving the system. The general equation of variable-mass motion is written as

In theoretical physics, relativistic Lagrangian mechanics is Lagrangian mechanics applied in the context of special relativity and general relativity.









