
In mathematics, a diffeomorphism is an isomorphism of differentiable manifolds. It is an invertible function that maps one differentiable manifold to another such that both the function and its inverse are continuously differentiable.

In mathematics and more specifically in topology, a homeomorphism, also called topological isomorphism, or bicontinuous function, is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are the mappings that preserve all the topological properties of a given space. Two spaces with a homeomorphism between them are called homeomorphic, and from a topological viewpoint they are the same.

In the part of mathematics referred to as topology, a surface is a two-dimensional manifold. Some surfaces arise as the boundaries of three-dimensional solid figures; for example, the sphere is the boundary of the solid ball. Other surfaces arise as graphs of functions of two variables; see the figure at right. However, surfaces can also be defined abstractly, without reference to any ambient space. For example, the Klein bottle is a surface that cannot be embedded in three-dimensional Euclidean space.

In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself.

In mathematics, low-dimensional topology is the branch of topology that studies manifolds, or more generally topological spaces, of four or fewer dimensions. Representative topics are the structure theory of 3-manifolds and 4-manifolds, knot theory, and braid groups. This can be regarded as a part of geometric topology. It may also be used to refer to the study of topological spaces of dimension 1, though this is more typically considered part of continuum theory.
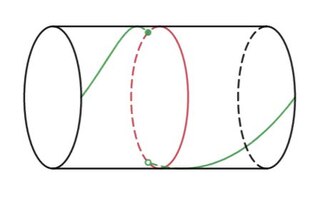
In geometric topology, a branch of mathematics, a Dehn twist is a certain type of self-homeomorphism of a surface.
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
In mathematics, the Lickorish–Wallace theorem in the theory of 3-manifolds states that any closed, orientable, connected 3-manifold may be obtained by performing Dehn surgery on a framed link in the 3-sphere with ±1 surgery coefficients. Furthermore, each component of the link can be assumed to be unknotted.
In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link. It is often conceptualized as two steps: drilling then filling.

In mathematics, triangulation describes the replacement of topological spaces by piecewise linear spaces, i.e. the choice of a homeomorphism in a suitable simplicial complex. Spaces being homeomorphic to a simplicial complex are called triangulable. Triangulation has various uses in different branches of mathematics, for instance in algebraic topology, in complex analysis or in modeling.
In mathematics, a fundamental polygon can be defined for every compact Riemann surface of genus greater than 0. It encodes not only information about the topology of the surface through its fundamental group but also determines the Riemann surface up to conformal equivalence. By the uniformization theorem, every compact Riemann surface has simply connected universal covering surface given by exactly one of the following:
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
The Heath-Brown–Moroz constantC, named for Roger Heath-Brown and Boris Moroz, is defined as
Douglas Geoffrey Northcott, FRS was a British mathematician who worked on ideal theory.
In mathematics, in the study of dynamical systems, the Hartman–Grobman theorem or linearisation theorem is a theorem about the local behaviour of dynamical systems in the neighbourhood of a hyperbolic equilibrium point. It asserts that linearisation—a natural simplification of the system—is effective in predicting qualitative patterns of behaviour. The theorem owes its name to Philip Hartman and David M. Grobman.
Patrick du Val was a British mathematician, known for his work on algebraic geometry, differential geometry, and general relativity. The concept of Du Val singularity of an algebraic surface is named after him.

William Bernard Raymond Lickorish is a mathematician. He is emeritus professor of geometric topology in the Department of Pure Mathematics and Mathematical Statistics, University of Cambridge, and also an emeritus fellow of Pembroke College, Cambridge. His research interests include topology and knot theory. He was one of the discoverers of the HOMFLY polynomial invariant of links, and proved the Lickorish-Wallace theorem which states that all closed orientable 3-manifolds can be obtained by Dehn surgery on a link.
In algebraic geometry, a Du Val singularity, also called simple surface singularity, Kleinian singularity, or rational double point, is an isolated singularity of a complex surface which is modeled on a double branched cover of the plane, with minimal resolution obtained by replacing the singular point with a tree of smooth rational curves, with intersection pattern dual to a Dynkin diagram of A-D-E singularity type. They are the canonical singularities in dimension 2. They were studied by Patrick du Val and Felix Klein.

Robert Clark Penner is an American mathematician whose work in geometry and combinatorics has found applications in high-energy physics and more recently in theoretical biology. He is the son of Sol Penner, an aerospace engineer.

In knot theory, a field of mathematics, the Bing double of a knot is a link with two components which follow the pattern of the knot and "hook together". Bing doubles were introduced in Bing (1952) by their namesake, the American mathematician R. H. Bing. The Bing double of a slice knot is a slice link, though it is unknown whether the converse is true. The components of a Bing double bound disjoint Seifert surfaces.










