In the mathematical field of knot theory, the bracket polynomial (also known as the Kauffman bracket) is a polynomial invariant of framed links. Although it is not an invariant of knots or links (as it is not invariant under type I Reidemeister moves), a suitably "normalized" version yields the famous knot invariant called the Jones polynomial. The bracket polynomial plays an important role in unifying the Jones polynomial with other quantum invariants. In particular, Kauffman's interpretation of the Jones polynomial allows generalization to invariants of 3-manifolds.
The bracket polynomial was discovered by Louis Kauffman in 1987.
The bracket polynomial of any (unoriented) link diagram , denoted , is a polynomial in the variable , characterized by the three rules:
The pictures in the second rule represent brackets of the link diagrams which differ inside a disc as shown but are identical outside. The third rule means that adding a circle disjoint from the rest of the diagram multiplies the bracket of the remaining diagram by .
| Hyperbolic |
|
|---|---|
| Satellite | |
| Torus | |
| Invariants | |
| Notation and operations | |
| Other | |
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined together so that it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting the string or passing the string through itself.
In the mathematical field of knot theory, a knot invariant is a quantity defined for each knot which is the same for equivalent knots. The equivalence is often given by ambient isotopy but can be given by homeomorphism. Some invariants are indeed numbers, but invariants can range from the simple, such as a yes/no answer, to those as complex as a homology theory. Research on invariants is not only motivated by the basic problem of distinguishing one knot from another but also to understand fundamental properties of knots and their relations to other branches of mathematics.
In the mathematical field of knot theory, a knot polynomial is a knot invariant in the form of a polynomial whose coefficients encode some of the properties of a given knot.
Skein relations are a mathematical tool used to study knots. A central question in the mathematical theory of knots is whether two knot diagrams represent the same knot. One way to answer the question is using knot polynomials, which are invariants of the knot. If two diagrams have different polynomials, they represent different knots. In general, the converse does not hold.
In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.
In the mathematical field of knot theory, the HOMFLY polynomial or HOMFLYPT polynomial, sometimes called the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables m and l.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923. In 1969, John Conway showed a version of this polynomial, now called the Alexander–Conway polynomial, could be computed using a skein relation, although its significance was not realized until the discovery of the Jones polynomial in 1984. Soon after Conway's reworking of the Alexander polynomial, it was realized that a similar skein relation was exhibited in Alexander's paper on his polynomial.
In mathematics, Khovanov homology is an oriented link invariant that arises as the homology of a chain complex. It may be regarded as a categorification of the Jones polynomial.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
In knot theory, a virtual knot is a generalization of knots in 3-dimensional Euclidean space, R3, to knots in thickened surfaces modulo an equivalence relation called stabilization/destabilization. Here is required to be closed and oriented. Virtual knots were first introduced by Kauffman (1999).
In the mathematical field of knot theory, the Arf invariant of a knot, named after Cahit Arf, is a knot invariant obtained from a quadratic form associated to a Seifert surface. If F is a Seifert surface of a knot, then the homology group H1(F, Z/2Z) has a quadratic form whose value is the number of full twists mod 2 in a neighborhood of an embedded circle representing an element of the homology group. The Arf invariant of this quadratic form is the Arf invariant of the knot.
In 3-dimensional topology, a part of the mathematical field of geometric topology, the Casson invariant is an integer-valued invariant of oriented integral homology 3-spheres, introduced by Andrew Casson.
Louis Hirsch Kauffman is an American mathematician, topologist, and professor of Mathematics in the Department of Mathematics, Statistics, and Computer science at the University of Illinois at Chicago. He is known for the introduction and development of the bracket polynomial and the Kauffman polynomial.
In the mathematical subject of knot theory, regular isotopy is the equivalence relation of link diagrams that is generated by using the 2nd and 3rd Reidemeister moves only. The notion of regular isotopy was introduced by Louis Kauffman. It can be thought of as an isotopy of a ribbon pressed flat against the plane which keeps the ribbon flat. For diagrams in the plane this is a finer equivalence relation than ambient isotopy of framed links, since the 2nd and 3rd Reidemeister moves preserve the winding number of the diagram. However, for diagrams in the sphere, the two notions are equivalent, due to the extra freedom of passing a strand through infinity.
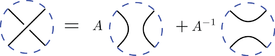
In knot theory, the Kauffman polynomial is a 2-variable knot polynomial due to Louis Kauffman. It is initially defined on a link diagram as
In the branch of mathematics called knot theory, the volume conjecture is the following open problem that relates quantum invariants of knots to the hyperbolic geometry of knot complements.
In computer science, the Aharonov–Jones–Landau algorithm is an efficient quantum algorithm for obtaining an additive approximation of the Jones polynomial of a given link at an arbitrary root of unity. Finding a multiplicative approximation is a #P-hard problem, so a better approximation is considered unlikely. However, it is known that computing an additive approximation of the Jones polynomial is a BQP-complete problem.
In the mathematical field of quantum topology, the Reshetikhin–Turaev invariants (RT-invariants) are a family of quantum invariants of framed links. Such invariants of framed links also give rise to invariants of 3-manifolds via the Dehn surgery construction. These invariants were discovered by Nicolai Reshetikhin and Vladimir Turaev in 1991, and were meant to be a mathematical realization of Witten's proposed invariants of links and 3-manifolds using quantum field theory.
