
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing it through itself.

DBLP is a computer science bibliography website. Starting in 1993 at Universität Trier in Germany, it grew from a small collection of HTML files and became an organization hosting a database and logic programming bibliography site. Since November 2018, DBLP is a branch of Schloss Dagstuhl – Leibniz-Zentrum für Informatik (LZI). DBLP listed more than 5.4 million journal articles, conference papers, and other publications on computer science in December 2020, up from about 14,000 in 1995 and 3.66 million in July 2016. All important journals on computer science are tracked. Proceedings papers of many conferences are also tracked. It is mirrored at three sites across the Internet.

In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.

In knot theory, a knot or link diagram is alternating if the crossings alternate under, over, under, over, as one travels along each component of the link. A link is alternating if it has an alternating diagram.

Dagstuhl is a computer science research center in Germany, located in and named after a district of the town of Wadern, Merzig-Wadern, Saarland.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
In the mathematical field of knot theory, a chiral knot is a knot that is not equivalent to its mirror image. An oriented knot that is equivalent to its mirror image is an amphicheiral knot, also called an achiral knot. The chirality of a knot is a knot invariant. A knot's chirality can be further classified depending on whether or not it is invertible.

In the mathematical field of knot theory, the Dowker–Thistlethwaite (DT) notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and Morwen Thistlethwaite, who refined a notation originally due to Peter Guthrie Tait.
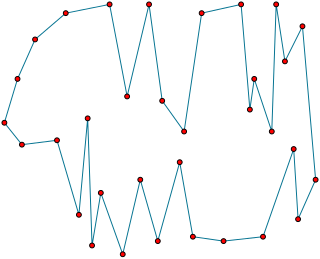
In computational geometry, a bitonic tour of a set of point sites in the Euclidean plane is a closed polygonal chain that has each site as one of its vertices, such that any vertical line crosses the chain at most twice.
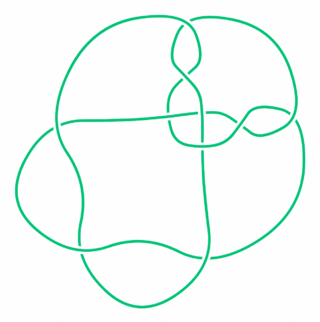
In the mathematical theory of knots, the Perko pair, named after Kenneth Perko, is a pair of entries in classical knot tables that actually represent the same knot. In Dale Rolfsen's knot table, this supposed pair of distinct knots is labeled 10161 and 10162. In 1973, while working to complete the classification by knot type of the Tait–Little knot tables of knots up to 10 crossings (dating from the late 19th century), Perko found the duplication in Charles Newton Little's table. This duplication had been missed by John Horton Conway several years before in his knot table and subsequently found its way into Rolfsen's table. The Perko pair gives a counterexample to a "theorem" claimed by Little in 1900 that the writhe of a reduced diagram of a knot is an invariant (see Tait conjectures), as the two diagrams for the pair have different writhes.
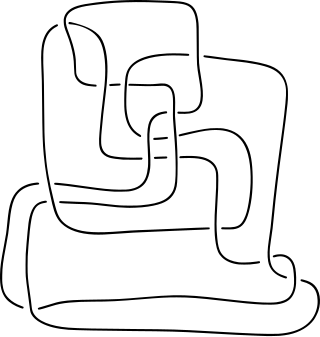
Morwen Bernard Thistlethwaite is a knot theorist and professor of mathematics for the University of Tennessee in Knoxville. He has made important contributions to both knot theory and Rubik's Cube group theory.
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.

Knots have been used for basic purposes such as recording information, fastening and tying objects together, for thousands of years. The early, significant stimulus in knot theory would arrive later with Sir William Thomson and his vortex theory of the atom.
The European Symposium on Algorithms (ESA) is an international conference covering the field of algorithms. It has been held annually since 1993, typically in early Autumn in a different European location each year. Like most theoretical computer science conferences its contributions are strongly peer-reviewed; the articles appear in proceedings published in Springer Lecture Notes in Computer Science. Acceptance rate of ESA is 24% in 2012 in both Design and Analysis and Engineering and Applications tracks.

In combinatorial mathematics, the ménage problem or problème des ménages asks for the number of different ways in which it is possible to seat a set of male-female couples at a round dining table so that men and women alternate and nobody sits next to his or her partner. This problem was formulated in 1891 by Édouard Lucas and independently, a few years earlier, by Peter Guthrie Tait in connection with knot theory. For a number of couples equal to 3, 4, 5, ... the number of seating arrangements is
The vortex theory of the atom was a 19th-century attempt by William Thomson to explain why the atoms recently discovered by chemists came in only relatively few varieties but in very great numbers of each kind. Based on the idea of stable, knotted vortices in the ether or aether, it contributed an important mathematical legacy.
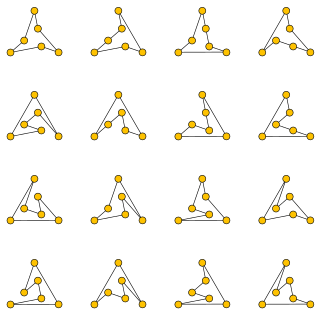
In computational geometry, a polygonalization of a finite set of points in the Euclidean plane is a simple polygon with the given points as its vertices. A polygonalization may also be called a polygonization, simple polygonalization, Hamiltonian polygon, non-crossing Hamiltonian cycle, or crossing-free straight-edge spanning cycle.
Gauss notation is a notation for mathematical knots. It is created by enumerating and classifying the crossings of an embedding of the knot in a plane. It is named after the German mathematician Carl Friedrich Gauss (1777–1855).
Mary Gertrude Haseman was an American mathematician known for her work in knot theory.












