In the mathematical field of topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be undone, the simplest knot being a ring. In mathematical language, a knot is an embedding of a circle in 3-dimensional Euclidean space, . Two mathematical knots are equivalent if one can be transformed into the other via a deformation of upon itself ; these transformations correspond to manipulations of a knotted string that do not involve cutting it or passing through itself.
In mathematics, a knot is an embedding of the circle S1 into three-dimensional Euclidean space, R3. Often two knots are considered equivalent if they are ambient isotopic, that is, if there exists a continuous deformation of R3 which takes one knot to the other.
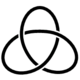
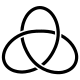
In knot theory, a branch of mathematics, the trefoil knot is the simplest example of a nontrivial knot. The trefoil can be obtained by joining together the two loose ends of a common overhand knot, resulting in a knotted loop. As the simplest knot, the trefoil is fundamental to the study of mathematical knot theory.
In mathematics, in the subfield of geometric topology, the mapping class group is an important algebraic invariant of a topological space. Briefly, the mapping class group is a certain discrete group corresponding to symmetries of the space.
In the mathematical field of knot theory, the HOMFLY polynomial or HOMFLYPT polynomial, sometimes called the generalized Jones polynomial, is a 2-variable knot polynomial, i.e. a knot invariant in the form of a polynomial of variables m and l.
In the mathematical field of knot theory, the Jones polynomial is a knot polynomial discovered by Vaughan Jones in 1984. Specifically, it is an invariant of an oriented knot or link which assigns to each oriented knot or link a Laurent polynomial in the variable with integer coefficients.
In geometry, a figure is chiral if it is not identical to its mirror image, or, more precisely, if it cannot be mapped to its mirror image by rotations and translations alone. An object that is not chiral is said to be achiral.
In knot theory, a knot or link diagram is alternating if the crossings alternate under, over, under, over, as one travels along each component of the link. A link is alternating if it has an alternating diagram.
In the mathematical theory of knots, a pretzel link is a special kind of link. It consists of a finite number tangles made of two intertwined circular helices, The tangles are connected cyclicly, the first component of the first tangle is connected to the second component of the second tangle, etc., with the first component of the last tangle connected to the second component of the first. A pretzel link which is also a knot is a pretzel knot.
The Tait conjectures are three conjectures made by 19th-century mathematician Peter Guthrie Tait in his study of knots. The Tait conjectures involve concepts in knot theory such as alternating knots, chirality, and writhe. All of the Tait conjectures have been solved, the most recent being the Flyping conjecture.
A slice knot is a mathematical knot in 3-dimensional space that bounds an embedded disk in 4-dimensional space.
In the mathematical field of knot theory, the Dowker–Thistlethwaite (DT) notation or code, for a knot is a sequence of even integers. The notation is named after Clifford Hugh Dowker and Morwen Thistlethwaite, who refined a notation originally due to Peter Guthrie Tait.
In knot theory, a Lissajous knot is a knot defined by parametric equations of the form
In the mathematical theory of knots, a flype is a kind of manipulation of knot and link diagrams used in the Tait flyping conjecture. It consists of twisting a part of a knot, a tangle T, by 180 degrees. Flype comes from a Scots word meaning to fold or to turn back. Two reduced alternating diagrams of an alternating link can be transformed to each other using flypes. This is the Tait flyping conjecture, proven in 1991 by Morwen Thistlethwaite and William Menasco.
In mathematics, especially in the area of topology known as knot theory, an invertible knot is a knot that can be continuously deformed to itself, but with its orientation reversed. A non-invertible knot is any knot which does not have this property. The invertibility of a knot is a knot invariant. An invertible link is the link equivalent of an invertible knot.
Knots have been used for basic purposes such as recording information, fastening and tying objects together, for thousands of years. The early, significant stimulus in knot theory would arrive later with Sir William Thomson and his vortex theory of the atom.
Ever since Sir William Thomson's vortex theory, mathematicians have tried to classify and tabulate all possible knots. As of May 2008, all prime knots up to 16 crossings have been tabulated. The major challenge of the process is that many apparently different knots may actually be different geometrical presentations of the same topological entity, and that proving or disproving knot equivalence is much more difficult than it at first seems.
In algebraic topology, a peripheral subgroup for a space-subspace pair X ⊃ Y is a certain subgroup of the fundamental group of the complementary space, π1(X − Y). Its conjugacy class is an invariant of the pair (X,Y). That is, any homeomorphism (X, Y) → (X′, Y′) induces an isomorphism π1(X − Y) → π1(X′ − Y′) taking peripheral subgroups to peripheral subgroups.
Mary Gertrude Haseman was an American mathematician known for her work in knot theory.
The left-handed trefoil knot.
The right-handed trefoil knot.
