The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).

In fluid dynamics, potential flow is the ideal flow pattern of an inviscid fluid. Potential flows are described and determined by mathematical methods.

In fluid dynamics, a vortex is a region in a fluid in which the flow revolves around an axis line, which may be straight or curved. Vortices form in stirred fluids, and may be observed in smoke rings, whirlpools in the wake of a boat, and the winds surrounding a tropical cyclone, tornado or dust devil.
The vorticity equation of fluid dynamics describes the evolution of the vorticity ω of a particle of a fluid as it moves with its flow; that is, the local rotation of the fluid. The governing equation is:
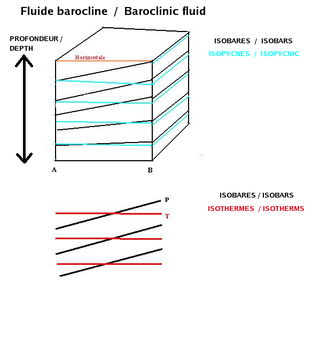
In fluid dynamics, the baroclinity of a stratified fluid is a measure of how misaligned the gradient of pressure is from the gradient of density in a fluid. In meteorology a baroclinic flow is one in which the density depends on both temperature and pressure. A simpler case, barotropic flow, allows for density dependence only on pressure, so that the curl of the pressure-gradient force vanishes.
In fluid dynamics, Stokes' law is an empirical law for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. It was derived by George Gabriel Stokes in 1851 by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.
In fluid mechanics, Helmholtz's theorems, named after Hermann von Helmholtz, describe the three-dimensional motion of fluid in the vicinity of vortex lines. These theorems apply to inviscid flows and flows where the influence of viscous forces are small and can be ignored.
In fluid mechanics, the Taylor–Proudman theorem states that when a solid body is moved slowly within a fluid that is steadily rotated with a high angular velocity , the fluid velocity will be uniform along any line parallel to the axis of rotation. must be large compared to the movement of the solid body in order to make the Coriolis force large compared to the acceleration terms.
In fluid dynamics, helicity is, under appropriate conditions, an invariant of the Euler equations of fluid flow, having a topological interpretation as a measure of linkage and/or knottedness of vortex lines in the flow. This was first proved by Jean-Jacques Moreau in 1961 and Moffatt derived it in 1969 without the knowledge of Moreau's paper. This helicity invariant is an extension of Woltjer's theorem for magnetic helicity.
In fluid mechanics, potential vorticity (PV) is a quantity which is proportional to the dot product of vorticity and stratification. This quantity, following a parcel of air or water, can only be changed by diabatic or frictional processes. It is a useful concept for understanding the generation of vorticity in cyclogenesis, especially along the polar front, and in analyzing flow in the ocean.

In physics, a quantum vortex represents a quantized flux circulation of some physical quantity. In most cases, quantum vortices are a type of topological defect exhibited in superfluids and superconductors. The existence of quantum vortices was first predicted by Lars Onsager in 1949 in connection with superfluid helium. Onsager reasoned that quantisation of vorticity is a direct consequence of the existence of a superfluid order parameter as a spatially continuous wavefunction. Onsager also pointed out that quantum vortices describe the circulation of superfluid and conjectured that their excitations are responsible for superfluid phase transitions. These ideas of Onsager were further developed by Richard Feynman in 1955 and in 1957 were applied to describe the magnetic phase diagram of type-II superconductors by Alexei Alexeyevich Abrikosov. In 1935 Fritz London published a very closely related work on magnetic flux quantization in superconductors. London's fluxoid can also be viewed as a quantum vortex.
The derivation of the Navier–Stokes equations as well as its application and formulation for different families of fluids, is an important exercise in fluid dynamics with applications in mechanical engineering, physics, chemistry, heat transfer, and electrical engineering. A proof explaining the properties and bounds of the equations, such as Navier–Stokes existence and smoothness, is one of the important unsolved problems in mathematics.
The Cauchy momentum equation is a vector partial differential equation put forth by Cauchy that describes the non-relativistic momentum transport in any continuum.
In fluid dynamics, the Oseen equations describe the flow of a viscous and incompressible fluid at small Reynolds numbers, as formulated by Carl Wilhelm Oseen in 1910. Oseen flow is an improved description of these flows, as compared to Stokes flow, with the (partial) inclusion of convective acceleration.

In fluid dynamics, the mild-slope equation describes the combined effects of diffraction and refraction for water waves propagating over bathymetry and due to lateral boundaries—like breakwaters and coastlines. It is an approximate model, deriving its name from being originally developed for wave propagation over mild slopes of the sea floor. The mild-slope equation is often used in coastal engineering to compute the wave-field changes near harbours and coasts.

In fluid dynamics, vortex stretching is the lengthening of vortices in three-dimensional fluid flow, associated with a corresponding increase of the component of vorticity in the stretching direction—due to the conservation of angular momentum.
The viscous vortex domains (VVD) method is a mesh-free method of computational fluid dynamics for directly numerically solving 2D Navier-Stokes equations in Lagrange coordinates. It doesn't implement any turbulence model and free of arbitrary parameters. The main idea of this method is to present vorticity field with discrete regions (domains), which travel with diffusive velocity relatively to fluid and conserve their circulation. The same approach was used in Diffusion Velocity method of Ogami and Akamatsu, but VVD uses other discrete formulas
In fluid dynamics, the Burgers vortex or Burgers–Rott vortex is an exact solution to the Navier–Stokes equations governing viscous flow, named after Jan Burgers and Nicholas Rott. The Burgers vortex describes a stationary, self-similar flow. An inward, radial flow, tends to concentrate vorticity in a narrow column around the symmetry axis, while an axial stretching causes the vorticity to increase. At the same time, viscous diffusion tends to spread the vorticity. The stationary Burgers vortex arises when the three effects are in balance.
The Lambda2 method, or Lambda2 vortex criterion, is a vortex core line detection algorithm that can adequately identify vortices from a three-dimensional fluid velocity field. The Lambda2 method is Galilean invariant, which means it produces the same results when a uniform velocity field is added to the existing velocity field or when the field is translated.
In fluid dynamics, Beltrami flows are flows in which the vorticity vector and the velocity vector are parallel to each other. In other words, Beltrami flow is a flow where Lamb vector is zero. It is named after the Italian mathematician Eugenio Beltrami due to his derivation of the Beltrami vector field, while initial developments in fluid dynamics were done by the Russian scientist Ippolit S. Gromeka in 1881.