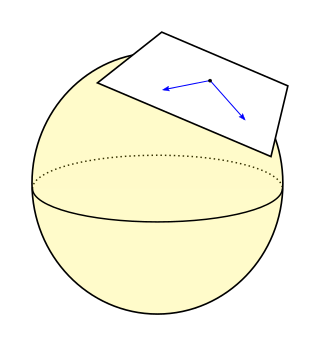
In mathematics, the tangent space of a manifold is a generalization of tangent lines to curves in two-dimensional space and tangent planes to surfaces in three-dimensional space in higher dimensions. In the context of physics the tangent space to a manifold at a point can be viewed as the space of possible velocities for a particle moving on the manifold.
In differential geometry, a Riemannian manifold is a geometric space on which many geometric notions such as distance, angles, length, volume, and curvature are defined. Euclidean space, the -sphere, hyperbolic space, and smooth surfaces in three-dimensional space, such as ellipsoids and paraboloids, are all examples of Riemannian manifolds. Riemannian manifolds are named after German mathematician Bernhard Riemann, who first conceptualized them.
In mathematics, complex geometry is the study of geometric structures and constructions arising out of, or described by, the complex numbers. In particular, complex geometry is concerned with the study of spaces such as complex manifolds and complex algebraic varieties, functions of several complex variables, and holomorphic constructions such as holomorphic vector bundles and coherent sheaves. Application of transcendental methods to algebraic geometry falls in this category, together with more geometric aspects of complex analysis.
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, is a geometric object which is determined by a choice of Riemannian or pseudo-Riemannian metric on a manifold. It can be considered, broadly, as a measure of the degree to which the geometry of a given metric tensor differs locally from that of ordinary Euclidean space or pseudo-Euclidean space.

In the mathematical disciplines of topology and geometry, an orbifold is a generalization of a manifold. Roughly speaking, an orbifold is a topological space which is locally a finite group quotient of a Euclidean space.
In mathematics, a submersion is a differentiable map between differentiable manifolds whose differential is everywhere surjective. This is a basic concept in differential topology. The notion of a submersion is dual to the notion of an immersion.

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.
This is a glossary of some terms used in Riemannian geometry and metric geometry — it doesn't cover the terminology of differential topology.
In mathematics, the Schwarzian derivative is an operator similar to the derivative which is invariant under Möbius transformations. Thus, it occurs in the theory of the complex projective line, and in particular, in the theory of modular forms and hypergeometric functions. It plays an important role in the theory of univalent functions, conformal mapping and Teichmüller spaces. It is named after the German mathematician Hermann Schwarz.

In differential geometry, the holonomy of a connection on a smooth manifold is the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. Holonomy is a general geometrical consequence of the curvature of the connection. For flat connections, the associated holonomy is a type of monodromy and is an inherently global notion. For curved connections, holonomy has nontrivial local and global features.
In mathematics and physics, the Christoffel symbols are an array of numbers describing a metric connection. The metric connection is a specialization of the affine connection to surfaces or other manifolds endowed with a metric, allowing distances to be measured on that surface. In differential geometry, an affine connection can be defined without reference to a metric, and many additional concepts follow: parallel transport, covariant derivatives, geodesics, etc. also do not require the concept of a metric. However, when a metric is available, these concepts can be directly tied to the "shape" of the manifold itself; that shape is determined by how the tangent space is attached to the cotangent space by the metric tensor. Abstractly, one would say that the manifold has an associated (orthonormal) frame bundle, with each "frame" being a possible choice of a coordinate frame. An invariant metric implies that the structure group of the frame bundle is the orthogonal group O(p, q). As a result, such a manifold is necessarily a (pseudo-)Riemannian manifold. The Christoffel symbols provide a concrete representation of the connection of (pseudo-)Riemannian geometry in terms of coordinates on the manifold. Additional concepts, such as parallel transport, geodesics, etc. can then be expressed in terms of Christoffel symbols.

In differential geometry, pushforward is a linear approximation of smooth maps on tangent spaces. Suppose that is a smooth map between smooth manifolds; then the differential of at a point , denoted , is, in some sense, the best linear approximation of near . It can be viewed as a generalization of the total derivative of ordinary calculus. Explicitly, the differential is a linear map from the tangent space of at to the tangent space of at , . Hence it can be used to push tangent vectors on forward to tangent vectors on . The differential of a map is also called, by various authors, the derivative or total derivative of .

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
In differential geometry, normal coordinates at a point p in a differentiable manifold equipped with a symmetric affine connection are a local coordinate system in a neighborhood of p obtained by applying the exponential map to the tangent space at p. In a normal coordinate system, the Christoffel symbols of the connection vanish at the point p, thus often simplifying local calculations. In normal coordinates associated to the Levi-Civita connection of a Riemannian manifold, one can additionally arrange that the metric tensor is the Kronecker delta at the point p, and that the first partial derivatives of the metric at p vanish.
In mathematics, the Abel–Jacobi map is a construction of algebraic geometry which relates an algebraic curve to its Jacobian variety. In Riemannian geometry, it is a more general construction mapping a manifold to its Jacobi torus. The name derives from the theorem of Abel and Jacobi that two effective divisors are linearly equivalent if and only if they are indistinguishable under the Abel–Jacobi map.

In the theory of Lie groups, the exponential map is a map from the Lie algebra of a Lie group to the group, which allows one to recapture the local group structure from the Lie algebra. The existence of the exponential map is one of the primary reasons that Lie algebras are a useful tool for studying Lie groups.
Computational anatomy is an interdisciplinary field of biology focused on quantitative investigation and modelling of anatomical shapes variability. It involves the development and application of mathematical, statistical and data-analytical methods for modelling and simulation of biological structures.
In the mathematical subject of group theory, a co-Hopfian group is a group that is not isomorphic to any of its proper subgroups. The notion is dual to that of a Hopfian group, named after Heinz Hopf.
In mathematics, the Cartan–Ambrose–Hicks theorem is a theorem of Riemannian geometry, according to which the Riemannian metric is locally determined by the Riemann curvature tensor, or in other words, behavior of the curvature tensor under parallel translation determines the metric.
In mathematics, and especially differential geometry and mathematical physics, gauge theory is the general study of connections on vector bundles, principal bundles, and fibre bundles. Gauge theory in mathematics should not be confused with the closely related concept of a gauge theory in physics, which is a field theory which admits gauge symmetry. In mathematics theory means a mathematical theory, encapsulating the general study of a collection of concepts or phenomena, whereas in the physical sense a gauge theory is a mathematical model of some natural phenomenon.








































