In differential geometry, a Riemannian manifold or Riemannian space(M, g), so called after the German mathematician Bernhard Riemann, is a real, smooth manifold M equipped with a positive-definite inner product gp on the tangent space TpM at each point p.

Noether's theorem states that every continuous symmetry of the action of a physical system with conservative forces has a corresponding conservation law. This is the first of two theorems proven by mathematician Emmy Noether in 1915 and published in 1918. The action of a physical system is the integral over time of a Lagrangian function, from which the system's behavior can be determined by the principle of least action. This theorem only applies to continuous and smooth symmetries of physical space.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.

A tangent bundle is the collection of all of the tangent spaces for all points on a manifold, structured in a way that it forms a new manifold itself. Formally, in differential geometry, the tangent bundle of a differentiable manifold is a manifold which assembles all the tangent vectors in . As a set, it is given by the disjoint union of the tangent spaces of . That is,
In mathematics, differential forms provide a unified approach to define integrands over curves, surfaces, solids, and higher-dimensional manifolds. The modern notion of differential forms was pioneered by Élie Cartan. It has many applications, especially in geometry, topology and physics.
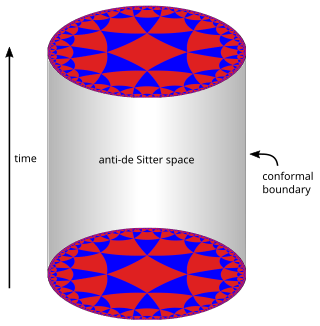
In mathematics and physics, n-dimensional anti-de Sitter space (AdSn) is a maximally symmetric Lorentzian manifold with constant negative scalar curvature. Anti-de Sitter space and de Sitter space are named after Willem de Sitter (1872–1934), professor of astronomy at Leiden University and director of the Leiden Observatory. Willem de Sitter and Albert Einstein worked together closely in Leiden in the 1920s on the spacetime structure of the universe. Paul Dirac was the first person to rigorously explore anti-de Sitter space, doing so in 1963.

In mathematics, a foliation is an equivalence relation on an n-manifold, the equivalence classes being connected, injectively immersed submanifolds, all of the same dimension p, modeled on the decomposition of the real coordinate space Rn into the cosets x + Rp of the standardly embedded subspace Rp. The equivalence classes are called the leaves of the foliation. If the manifold and/or the submanifolds are required to have a piecewise-linear, differentiable, or analytic structure then one defines piecewise-linear, differentiable, or analytic foliations, respectively. In the most important case of differentiable foliation of class Cr it is usually understood that r ≥ 1. The number p is called the dimension of the foliation and q = n − p is called its codimension.
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given by a principal connection on the frame bundle – see affine connection. In the special case of a manifold isometrically embedded into a higher-dimensional Euclidean space, the covariant derivative can be viewed as the orthogonal projection of the Euclidean directional derivative onto the manifold's tangent space. In this case the Euclidean derivative is broken into two parts, the extrinsic normal component and the intrinsic covariant derivative component.
In physics, the S-matrix or scattering matrix relates the initial state and the final state of a physical system undergoing a scattering process. It is used in quantum mechanics, scattering theory and quantum field theory (QFT).

In mathematical analysis, the smoothness of a function is a property measured by the number, called differentiability class, of continuous derivatives it has over its domain.

In mathematics, a differentiable manifold is a type of manifold that is locally similar enough to a vector space to allow one to apply calculus. Any manifold can be described by a collection of charts (atlas). One may then apply ideas from calculus while working within the individual charts, since each chart lies within a vector space to which the usual rules of calculus apply. If the charts are suitably compatible, then computations done in one chart are valid in any other differentiable chart.
In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space. Banach manifolds are one possibility of extending manifolds to infinite dimensions.
In mathematics, specifically in symplectic geometry, the momentum map is a tool associated with a Hamiltonian action of a Lie group on a symplectic manifold, used to construct conserved quantities for the action. The momentum map generalizes the classical notions of linear and angular momentum. It is an essential ingredient in various constructions of symplectic manifolds, including symplectic (Marsden–Weinstein) quotients, discussed below, and symplectic cuts and sums.
In mathematics, in particular in nonlinear analysis, a Fréchet manifold is a topological space modeled on a Fréchet space in much the same way as a manifold is modeled on a Euclidean space.
In mathematics, a holomorphic vector bundle is a complex vector bundle over a complex manifold X such that the total space E is a complex manifold and the projection map π : E → X is holomorphic. Fundamental examples are the holomorphic tangent bundle of a complex manifold, and its dual, the holomorphic cotangent bundle. A holomorphic line bundle is a rank one holomorphic vector bundle.
In many-body theory, the term Green's function is sometimes used interchangeably with correlation function, but refers specifically to correlators of field operators or creation and annihilation operators.
In mathematics, the Kodaira–Spencer map, introduced by Kunihiko Kodaira and Donald C. Spencer, is a map associated to a deformation of a scheme or complex manifold X, taking a tangent space of a point of the deformation space to the first cohomology group of the sheaf of vector fields on X.
Martin Hairer's theory of regularity structures provides a framework for studying a large class of subcritical parabolic stochastic partial differential equations arising from quantum field theory. The framework covers the Kardar–Parisi–Zhang equation, the equation and the parabolic Anderson model, all of which require renormalization in order to have a well-defined notion of solution.
In category theory and related fields of mathematics, an envelope is a construction that generalizes the operations of "exterior completion", like completion of a locally convex space, or Stone–Čech compactification of a topological space. A dual construction is called refinement.
In mathematics, and especially differential geometry and mathematical physics, gauge theory is the general study of connections on vector bundles, principal bundles, and fibre bundles. Gauge theory in mathematics should not be confused with the closely related concept of a gauge theory in physics, which is a field theory which admits gauge symmetry. In mathematics theory means a mathematical theory, encapsulating the general study of a collection of concepts or phenomena, whereas in the physical sense a gauge theory is a mathematical model of some natural phenomenon.





































