In mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.

In geometry, a Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, called coordinate lines, coordinate axes or just axes of the system. The point where the axes meet is called the origin and has (0, 0) as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame.

In mathematics, the slope or gradient of a line is a number that describes the direction of the line on a plane. Often denoted by the letter m, slope is calculated as the ratio of the vertical change to the horizontal change between two distinct points on the line, giving the same number for any choice of points.
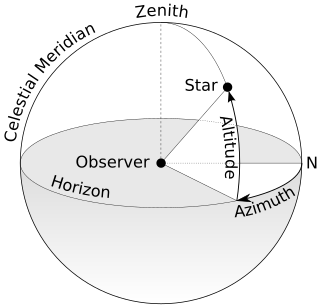
An azimuth is the horizontal angle from a cardinal direction, most commonly north, in a local or observer-centric spherical coordinate system.

In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation.

Apollonius of Perga was an ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the earlier contributions of Euclid and Archimedes on the topic, he brought them to the state prior to the invention of analytic geometry. His definitions of the terms ellipse, parabola, and hyperbola are the ones in use today. With his predecessors Euclid and Archimedes, Apollonius is generally considered among the greatest mathematicians of antiquity.

A 3D projection is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane.

In analytic geometry, using the common convention that the horizontal axis represents a variable and the vertical axis represents a variable , a -intercept or vertical intercept is a point where the graph of a function or relation intersects the -axis of the coordinate system. As such, these points satisfy .
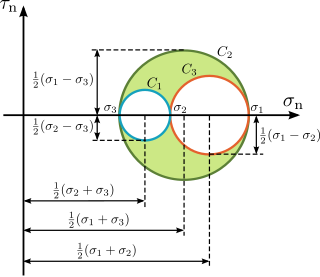
Mohr's circle is a two-dimensional graphical representation of the transformation law for the Cauchy stress tensor.

In classical geometry, a radius of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the Latin radius, meaning ray but also the spoke of a chariot wheel. The typical abbreviation and mathematical variable name for radius is R or r. By extension, the diameter D is defined as twice the radius:

In mathematics, a critical point is the argument of a function where the function derivative is zero . The value of the function at a critical point is a critical value.
Many letters of the Latin alphabet, both capital and small, are used in mathematics, science, and engineering to denote by convention specific or abstracted constants, variables of a certain type, units, multipliers, or physical entities. Certain letters, when combined with special formatting, take on special meaning.

In 2-dimensional geometry, a lens is a convex region bounded by two circular arcs joined to each other at their endpoints. In order for this shape to be convex, both arcs must bow outwards (convex-convex). This shape can be formed as the intersection of two circular disks. It can also be formed as the union of two circular segments, joined along a common chord.

In geometry, Poncelet's closure theorem, also known as Poncelet's porism, states that whenever a polygon is inscribed in one conic section and circumscribes another one, the polygon must be part of an infinite family of polygons that are all inscribed in and circumscribe the same two conics. It is named after French engineer and mathematician Jean-Victor Poncelet, who wrote about it in 1822; however, the triangular case was discovered significantly earlier, in 1746 by William Chapple.

In geometry, the hyperboloid model, also known as the Minkowski model after Hermann Minkowski, is a model of n-dimensional hyperbolic geometry in which points are represented by points on the forward sheet S+ of a two-sheeted hyperboloid in (n+1)-dimensional Minkowski space or by the displacement vectors from the origin to those points, and m-planes are represented by the intersections of (m+1)-planes passing through the origin in Minkowski space with S+ or by wedge products of m vectors. Hyperbolic space is embedded isometrically in Minkowski space; that is, the hyperbolic distance function is inherited from Minkowski space, analogous to the way spherical distance is inherited from Euclidean distance when the n-sphere is embedded in (n+1)-dimensional Euclidean space.

In mathematics, a Euclidean plane is a Euclidean space of dimension two, denoted or . It is a geometric space in which two real numbers are required to determine the position of each point. It is an affine space, which includes in particular the concept of parallel lines. It has also metrical properties induced by a distance, which allows to define circles, and angle measurement.

In cartography, the normal cylindrical equal-area projection is a family of normal cylindrical, equal-area map projections.

In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as S1 because it is a one-dimensional unit n-sphere.

In mathematics, a minimal surface of revolution or minimum surface of revolution is a surface of revolution defined from two points in a half-plane, whose boundary is the axis of revolution of the surface. It is generated by a curve that lies in the half-plane and connects the two points; among all the surfaces that can be generated in this way, it is the one that minimizes the surface area. A basic problem in the calculus of variations is finding the curve between two points that produces this minimal surface of revolution.
Pohlke's theorem is the fundamental theorem of axonometry. It was established 1853 by the German painter and teacher of descriptive geometry Karl Wilhelm Pohlke. The first proof of the theorem was published 1864 by the German mathematician Hermann Amandus Schwarz, who was a student of Pohlke. Therefore the theorem is sometimes called theorem of Pohlke and Schwarz, too.



















