In geometry, a Cartesian coordinate system in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, called coordinate lines, coordinate axes or just axes of the system. The point where the axes meet is called the origin and has (0, 0) as coordinates. The axes directions represent an orthogonal basis. The combination of origin and basis forms a coordinate frame called the Cartesian frame.

A gyroscope is a device used for measuring or maintaining orientation and angular velocity. It is a spinning wheel or disc in which the axis of rotation is free to assume any orientation by itself. When rotating, the orientation of this axis is unaffected by tilting or rotation of the mounting, according to the conservation of angular momentum.

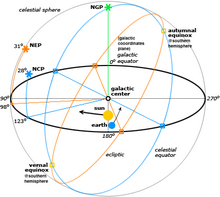
The equatorial coordinate system is a celestial coordinate system widely used to specify the positions of celestial objects. It may be implemented in spherical or rectangular coordinates, both defined by an origin at the centre of Earth, a fundamental plane consisting of the projection of Earth's equator onto the celestial sphere, a primary direction towards the March equinox, and a right-handed convention.

Flight dynamics is the science of air vehicle orientation and control in three dimensions. The three critical flight dynamics parameters are the angles of rotation in three dimensions about the vehicle's center of gravity (cg), known as pitch, roll and yaw. These are collectively known as aircraft attitude, often principally relative to the atmospheric frame in normal flight, but also relative to terrain during takeoff or landing, or when operating at low elevation. The concept of attitude is not specific to fixed-wing aircraft, but also extends to rotary aircraft such as helicopters, and dirigibles, where the flight dynamics involved in establishing and controlling attitude are entirely different.

Gimbal lock is the loss of one degree of freedom in a multi-dimensional mechanism at certain alignments of the axes. In a three-dimensional three-gimbal mechanism, gimbal lock occurs when the axes of two of the gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space.

The Euler angles are three angles introduced by Leonhard Euler to describe the orientation of a rigid body with respect to a fixed coordinate system.

In physics, a rigid body, also known as a rigid object, is a solid body in which deformation is zero or negligible. The distance between any two given points on a rigid body remains constant in time regardless of external forces or moments exerted on it. A rigid body is usually considered as a continuous distribution of mass.

In astrodynamics and celestial dynamics, the orbital state vectors of an orbit are Cartesian vectors of position and velocity that together with their time (epoch) uniquely determine the trajectory of the orbiting body in space.
The International Celestial Reference System (ICRS) is the current standard celestial reference system adopted by the International Astronomical Union (IAU). Its origin is at the barycenter of the Solar System, with axes that are intended to "show no global rotation with respect to a set of distant extragalactic objects". This fixed reference system differs from previous reference systems, which had been based on Catalogues of Fundamental Stars that had published the positions of stars based on direct "observations of [their] equatorial coordinates, right ascension and declination" and had adopted as "privileged axes ... the mean equator and the dynamical equinox" at a particular date and time.

In geometry, the orientation, attitude, bearing, direction, or angular position of an object – such as a line, plane or rigid body – is part of the description of how it is placed in the space it occupies. More specifically, it refers to the imaginary rotation that is needed to move the object from a reference placement to its current placement. A rotation may not be enough to reach the current placement, in which case it may be necessary to add an imaginary translation to change the object's position. The position and orientation together fully describe how the object is placed in space. The above-mentioned imaginary rotation and translation may be thought to occur in any order, as the orientation of an object does not change when it translates, and its position does not change when it rotates.

The Earth-centered, Earth-fixed coordinate system, also known as the geocentric coordinate system, is a cartesian spatial reference system that represents locations in the vicinity of the Earth as X, Y, and Z measurements from its center of mass. Its most common use is in tracking the orbits of satellites and in satellite navigation systems for measuring locations on the surface of the Earth, but it is also used in applications such as tracking crustal motion.

Local tangent plane coordinates (LTP) are part of a spatial reference system based on the tangent plane defined by the local vertical direction and the Earth's axis of rotation. They are also known as local ellipsoidal system, local geodetic coordinate system, local vertical, local horizontal coordinates (LVLH), or topocentric coordinates. It consists of three coordinates: one represents the position along the northern axis, one along the local eastern axis, and one represents the vertical position. Two right-handed variants exist: east, north, up (ENU) coordinates and north, east, down (NED) coordinates. They serve for representing state vectors that are commonly used in aviation and marine cybernetics.

Stability derivatives, and also control derivatives, are measures of how particular forces and moments on an aircraft change as other parameters related to stability change. For a defined "trim" flight condition, changes and oscillations occur in these parameters. Equations of motion are used to analyze these changes and oscillations. Stability and control derivatives are used to linearize (simplify) these equations of motion so the stability of the vehicle can be more readily analyzed.

An aircraft in flight is free to rotate in three dimensions: yaw, nose left or right about an axis running up and down; pitch, nose up or down about an axis running from wing to wing; and roll, rotation about an axis running from nose to tail. The axes are alternatively designated as vertical, lateral, and longitudinal respectively. These axes move with the vehicle and rotate relative to the Earth along with the craft. These definitions were analogously applied to spacecraft when the first crewed spacecraft were designed in the late 1950s.

Earth-centered inertial (ECI) coordinate frames have their origins at the center of mass of Earth and are fixed with respect to the stars. "I" in "ECI" stands for inertial, in contrast to the "Earth-centered – Earth-fixed" (ECEF) frames, which remains fixed with respect to Earth's surface in its rotation, and then rotates with respect to stars.

An inertial navigation system is a navigation device that uses motion sensors (accelerometers), rotation sensors (gyroscopes) and a computer to continuously calculate by dead reckoning the position, the orientation, and the velocity of a moving object without the need for external references. Often the inertial sensors are supplemented by a barometric altimeter and sometimes by magnetic sensors (magnetometers) and/or speed measuring devices. INSs are used on mobile robots and on vehicles such as ships, aircraft, submarines, guided missiles, and spacecraft. Older INS systems generally used an inertial platform as their mounting point to the vehicle and the terms are sometimes considered synonymous.

A yaw rotation is a movement around the yaw axis of a rigid body that changes the direction it is pointing, to the left or right of its direction of motion. The yaw rate or yaw velocity of a car, aircraft, projectile or other rigid body is the angular velocity of this rotation, or rate of change of the heading angle when the aircraft is horizontal. It is commonly measured in degrees per second or radians per second.
Spacecraft attitude control is the process of controlling the orientation of a spacecraft with respect to an inertial frame of reference or another entity such as the celestial sphere, certain fields, and nearby objects, etc.
In physics and engineering, Davenport chained rotations are three chained intrinsic rotations about body-fixed specific axes. Euler rotations and Tait–Bryan rotations are particular cases of the Davenport general rotation decomposition. The angles of rotation are called Davenport angles because the general problem of decomposing a rotation in a sequence of three was studied first by Paul B. Davenport.

Steady flight, unaccelerated flight, or equilibrium flight is a special case in flight dynamics where the aircraft's linear and angular velocity are constant in a body-fixed reference frame. Basic aircraft maneuvers such as level flight, climbs and descents, and coordinated turns can be modeled as steady flight maneuvers. Typical aircraft flight consists of a series of steady flight maneuvers connected by brief, accelerated transitions. Because of this, primary applications of steady flight models include aircraft design, assessment of aircraft performance, flight planning, and using steady flight states as the equilibrium conditions around which flight dynamics equations are expanded.