
In probability theory, the central limit theorem (CLT) states that, under appropriate conditions, the distribution of a normalized version of the sample mean converges to a standard normal distribution. This holds even if the original variables themselves are not normally distributed. There are several versions of the CLT, each applying in the context of different conditions.
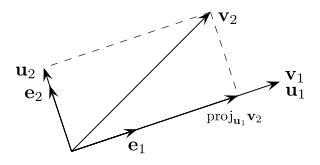
In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process or Gram-Schmidt algorithm is a way of finding a set of two or more vectors that are perpendicular to each other.
Controllability is an important property of a control system and plays a crucial role in many control problems, such as stabilization of unstable systems by feedback, or optimal control.
In the mathematical field of differential geometry, a metric tensor is an additional structure on a manifold M that allows defining distances and angles, just as the inner product on a Euclidean space allows defining distances and angles there. More precisely, a metric tensor at a point p of M is a bilinear form defined on the tangent space at p, and a metric field on M consists of a metric tensor at each point p of M that varies smoothly with p.
H∞methods are used in control theory to synthesize controllers to achieve stabilization with guaranteed performance. To use H∞ methods, a control designer expresses the control problem as a mathematical optimization problem and then finds the controller that solves this optimization. H∞ techniques have the advantage over classical control techniques in that H∞ techniques are readily applicable to problems involving multivariate systems with cross-coupling between channels; disadvantages of H∞ techniques include the level of mathematical understanding needed to apply them successfully and the need for a reasonably good model of the system to be controlled. It is important to keep in mind that the resulting controller is only optimal with respect to the prescribed cost function and does not necessarily represent the best controller in terms of the usual performance measures used to evaluate controllers such as settling time, energy expended, etc. Also, non-linear constraints such as saturation are generally not well-handled. These methods were introduced into control theory in the late 1970s-early 1980s by George Zames, J. William Helton , and Allen Tannenbaum.
In control systems, sliding mode control (SMC) is a nonlinear control method that alters the dynamics of a nonlinear system by applying a discontinuous control signal that forces the system to "slide" along a cross-section of the system's normal behavior. The state-feedback control law is not a continuous function of time. Instead, it can switch from one continuous structure to another based on the current position in the state space. Hence, sliding mode control is a variable structure control method. The multiple control structures are designed so that trajectories always move toward an adjacent region with a different control structure, and so the ultimate trajectory will not exist entirely within one control structure. Instead, it will slide along the boundaries of the control structures. The motion of the system as it slides along these boundaries is called a sliding mode and the geometrical locus consisting of the boundaries is called the sliding (hyper)surface. In the context of modern control theory, any variable structure system, like a system under SMC, may be viewed as a special case of a hybrid dynamical system as the system both flows through a continuous state space but also moves through different discrete control modes.
In control engineering and system identification, a state-space representation is a mathematical model of a physical system specified as a set of input, output, and variables related by first-order differential equations or difference equations. Such variables, called state variables, evolve over time in a way that depends on the values they have at any given instant and on the externally imposed values of input variables. Output variables’ values depend on the state variable values and may also depend on the input variable values.
In multivariable calculus, the implicit function theorem is a tool that allows relations to be converted to functions of several real variables. It does so by representing the relation as the graph of a function. There may not be a single function whose graph can represent the entire relation, but there may be such a function on a restriction of the domain of the relation. The implicit function theorem gives a sufficient condition to ensure that there is such a function.
In mathematics, the matrix exponential is a matrix function on square matrices analogous to the ordinary exponential function. It is used to solve systems of linear differential equations. In the theory of Lie groups, the matrix exponential gives the exponential map between a matrix Lie algebra and the corresponding Lie group.
In control theory, a state observer or state estimator is a system that provides an estimate of the internal state of a given real system, from measurements of the input and output of the real system. It is typically computer-implemented, and provides the basis of many practical applications.
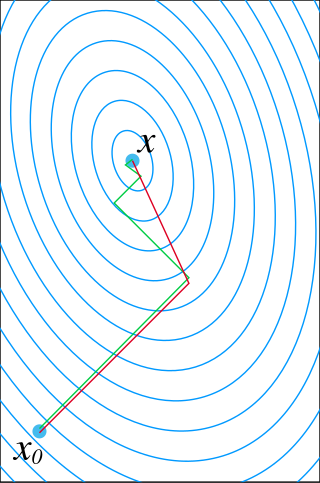
In mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is positive-semidefinite. The conjugate gradient method is often implemented as an iterative algorithm, applicable to sparse systems that are too large to be handled by a direct implementation or other direct methods such as the Cholesky decomposition. Large sparse systems often arise when numerically solving partial differential equations or optimization problems.
Full state feedback (FSF), or pole placement, is a method employed in feedback control system theory to place the closed-loop poles of a plant in predetermined locations in the s-plane. Placing poles is desirable because the location of the poles corresponds directly to the eigenvalues of the system, which control the characteristics of the response of the system. The system must be considered controllable in order to implement this method.

Feedback linearization is a common strategy employed in nonlinear control to control nonlinear systems. Feedback linearization techniques may be applied to nonlinear control systems of the form
In control theory, a control-Lyapunov function (CLF) is an extension of the idea of Lyapunov function to systems with control inputs. The ordinary Lyapunov function is used to test whether a dynamical system is (Lyapunov) stable or asymptotically stable. Lyapunov stability means that if the system starts in a state in some domain D, then the state will remain in D for all time. For asymptotic stability, the state is also required to converge to . A control-Lyapunov function is used to test whether a system is asymptotically stabilizable, that is whether for any state x there exists a control such that the system can be brought to the zero state asymptotically by applying the control u.
In classical mechanics, holonomic constraints are relations between the position variables that can be expressed in the following form:
Artstein's theorem states that a nonlinear dynamical system in the control-affine form
In control theory, dynamical systems are in strict-feedback form when they can be expressed as
Input-to-state stability (ISS) is a stability notion widely used to study stability of nonlinear control systems with external inputs. Roughly speaking, a control system is ISS if it is globally asymptotically stable in the absence of external inputs and if its trajectories are bounded by a function of the size of the input for all sufficiently large times. The importance of ISS is due to the fact that the concept has bridged the gap between input–output and state-space methods, widely used within the control systems community.
Dynamic Substructuring (DS) is an engineering tool used to model and analyse the dynamics of mechanical systems by means of its components or substructures. Using the dynamic substructuring approach one is able to analyse the dynamic behaviour of substructures separately and to later on calculate the assembled dynamics using coupling procedures. Dynamic substructuring has several advantages over the analysis of the fully assembled system:

In mathematics, orthogonality is the generalization of the geometric notion of perpendicularity to the linear algebra of bilinear forms.
























































































































































