Biorthogonal nearly coiflet basis

Last updated April 07, 2021

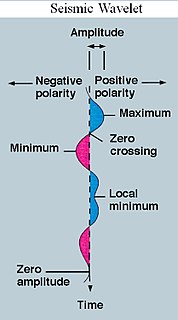
In applied mathematics, biorthogonal nearly coiflet bases are wavelet bases proposed by Lowell L. Winger. The wavelet is based on biorthogonal coiflet wavelet bases, but sacrifices its regularity to increase the filter's bandwidth, which might lead to better image compression performance.

Motivation

Nowadays, a large amount of information is stored, processed, and delivered, so the method of data compressing — especially for images — becomes more significant. Since wavelet transforms can deal with signals in both space and frequency domains, they compensate for the deficiency of Fourier transforms and emerged as a potential technique for image processing.^[1]

Traditional wavelet filter design prefers filters with high regularity and smoothness to perform image compression.^[2] Coiflets are such a kind of filter which emphasizes the vanishing moments of both the wavelet and scaling function, and can be achieved by maximizing the total number of vanishing moments and distributing them between the analysis and synthesis low pass filters. The property of vanishing moments enables the wavelet series of the signal to be a sparse presentation, which is the reason why wavelets can be applied for image compression.^[3] Besides orthogonal filter banks, biorthogonal wavelets with maximized vanishing moments have also been proposed.^[4] However, regularity and smoothness are not sufficient for excellent image compression.^[5] Common filter banks prefer filters with high regularity, flat passbands and stopbands, and a narrow transition zone, while Pixstream Incorporated proposed filters with wider passband by sacrificing their regularity and passband flatness.^[5]

Theory

The biorthogonal wavelet base contains two wavelet functions, $\psi (t)$ and its couple wavelet ${\tilde {\psi }}(t)$ , while $\psi (t)$ relates to the lowpass analysis filter $H0$ and the high pass analysis filter $G0$ . Similarly, ${\tilde {\psi }}(t)$ relates to the lowpass synthesis filter ${\tilde {H}}0$ and the high pass synthesis filter ${\tilde {G0}}$ . For biorthogonal wavelet base, $H0$ and ${\tilde {G0}}$ are orthogonal; Likewise, $G0$ and ${\tilde {H0}}$ are orthogonal, too.

In order to construct a biorthogonal nearly coiflet base, the Pixstream Incorporated begins with the (max flat) biorthogonal coiflet base.^[5] Decomposing and reconstructing low-pass filters expressed by Bernstein polynomials ensures that the coefficients of filters are symmetric, which benefits the image processing: If the phase of real-valued function is symmetry, than the function has generalized linear phase, and since the human eyes are sensitive to symmetrical error, wavelet base with linear phase is better for image processing application.^[1]

Recall that the Bernstein polynomials are defined as below:

B_{k}^{n}(x)=(_{k}^{n})x^{k}(1-x)^{n-k}{\text{ for }}k=1,2,\ldots ,n,

which can be considered as a polynomial f(x) over the interval $x\in [0,1]$ .^[6] Besides, the Bernstein form of a general polynomial is expressed by

H1(x)=\sum _{k=0}^{n}d(k)(_{k}^{n})x^{k}(1-x)^{n-k},

where d(i) are the Bernstein coefficients. Note that the number of zeros in Bernstein coefficients determines the vanishing moments of wavelet functions.^[7] By sacrificing a zero of the Bernstein-basis filter at $\omega =\pi$ (which sacrifices its regularity and flatness), the filter is no longer coiflet but nearly coiflet.^[5] Then, the magnitude of the highest-order non-zero Bernstein basis coefficient is increased, which leads to a wider passband. On the other hand, to perform image compression and reconstruction, analysis filters are determined by synthesis filters. Since the designed filter has a lower regularity, worse flatness and wider passband, the resulting dual low pass filter has a higher regularity, better flatness and narrower passband. Besides, if the passband of the starting biorthogonal coiflet is narrower than the target synthesis filter G0, then its passband is widened only enough to match G0 in order to minimize the impact on smoothness (i.e. the analysis filter H0 is not invariably the design filter). Similarly, if the original coiflet is wider than the target G0, than the original filter's passband is adjusted to match the analysis filter H0. Therefore, the analysis and synthesis filters have similar bandwidth.

The ringing effect (overshoot and undershoot) and shift-variance of image compression might be alleviated by balancing the passband of the analysis and synthesis filters. In other word, the smoothest or highest regularity filters are not always the best choices for synthesis low pass filters.

Drawback

The idea of this method is to obtain more free parameters by despairing some vanishing elements. However, this technique cannot unify biorthogonal wavelet filter banks with different taps into a closed-form expression based on one degree of freedom.^[8]

Related Research Articles

A wavelet is a wave-like oscillation with an amplitude that begins at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one recorded by a seismograph or heart monitor. Generally, wavelets are intentionally crafted to have specific properties that make them useful for signal processing.

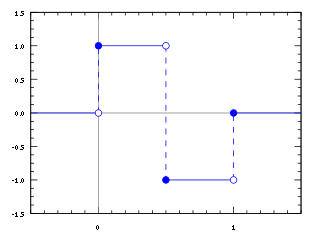
In mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal basis. The Haar sequence is now recognised as the first known wavelet basis and extensively used as a teaching example.

In digital signal processing, a quadrature mirror filter is a filter whose magnitude response is the mirror image around $of that of another filter. Together these filters, first introduced by Croisier et al., are known as the Quadrature Mirror Filter pair.$

Pseudo-spectral methods, also known as discrete variable representation (DVR) methods, are a class of numerical methods used in applied mathematics and scientific computing for the solution of partial differential equations. They are closely related to spectral methods, but complement the basis by an additional pseudo-spectral basis, which allows representation of functions on a quadrature grid. This simplifies the evaluation of certain operators, and can considerably speed up the calculation when using fast algorithms such as the fast Fourier transform.

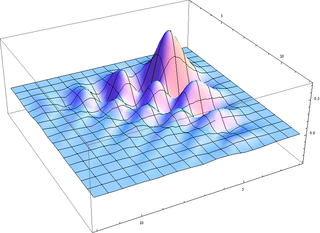
The Daubechies wavelets, based on the work of Ingrid Daubechies, are a family of orthogonal wavelets defining a discrete wavelet transform and characterized by a maximal number of vanishing moments for some given support. With each wavelet type of this class, there is a scaling function which generates an orthogonal multiresolution analysis.

In mathematics, the continuous wavelet transform (CWT) is a formal tool that provides an overcomplete representation of a signal by letting the translation and scale parameter of the wavelets vary continuously.

In numerical analysis and functional analysis, a discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution: it captures both frequency and location information.

In signal processing, a filter bank is an array of bandpass filters that separates the input signal into multiple components, each one carrying a single frequency sub-band of the original signal. One application of a filter bank is a graphic equalizer, which can attenuate the components differently and recombine them into a modified version of the original signal. The process of decomposition performed by the filter bank is called analysis ; the output of analysis is referred to as a subband signal with as many subbands as there are filters in the filter bank. The reconstruction process is called synthesis, meaning reconstitution of a complete signal resulting from the filtering process.

The Fast Wavelet Transform is a mathematical algorithm designed to turn a waveform or signal in the time domain into a sequence of coefficients based on an orthogonal basis of small finite waves, or wavelets. The transform can be easily extended to multidimensional signals, such as images, where the time domain is replaced with the space domain. This algorithm was introduced in 1989 by Stéphane Mallat.

Coiflets are discrete wavelets designed by Ingrid Daubechies, at the request of Ronald Coifman, to have scaling functions with vanishing moments. The wavelet is near symmetric, their wavelet functions have $vanishing moments and scaling functions, and has been used in many applications using Calderón-Zygmund operators.$

A multiresolution analysis (MRA) or multiscale approximation (MSA) is the design method of most of the practically relevant discrete wavelet transforms (DWT) and the justification for the algorithm of the fast wavelet transform (FWT). It was introduced in this context in 1988/89 by Stephane Mallat and Yves Meyer and has predecessors in the microlocal analysis in the theory of differential equations and the pyramid methods of image processing as introduced in 1981/83 by Peter J. Burt, Edward H. Adelson and James L. Crowley.

Cohen–Daubechies–Feauveau wavelets are a family of biorthogonal wavelets that was made popular by Ingrid Daubechies. These are not the same as the orthogonal Daubechies wavelets, and also not very similar in shape and properties. However, their construction idea is the same.

In mathematics, a wavelet series is a representation of a square-integrable function by a certain orthonormal series generated by a wavelet. This article provides a formal, mathematical definition of an orthonormal wavelet and of the integral wavelet transform.

An orthogonal wavelet is a wavelet whose associated wavelet transform is orthogonal. That is, the inverse wavelet transform is the adjoint of the wavelet transform. If this condition is weakened one may end up with biorthogonal wavelets.

In mathematics, a dual wavelet is the dual to a wavelet. In general, the wavelet series generated by a square-integrable function will have a dual series, in the sense of the Riesz representation theorem. However, the dual series is not itself in general representable by a square-integrable function.

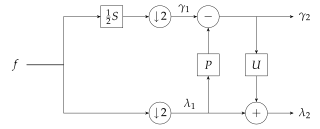
The lifting scheme is a technique for both designing wavelets and performing the discrete wavelet transform (DWT). In an implementation, it is often worthwhile to merge these steps and design the wavelet filters while performing the wavelet transform. This is then called the second-generation wavelet transform. The technique was introduced by Wim Sweldens.

A Biorthogonal wavelet is a wavelet where the associated wavelet transform is invertible but not necessarily orthogonal. Designing biorthogonal wavelets allows more degrees of freedom than orthogonal wavelets. One additional degree of freedom is the possibility to construct symmetric wavelet functions.

In mathematics, in the area of wavelet analysis, a refinable function is a function which fulfils some kind of self-similarity. A function $is called refinable with respect to the mask if$

In applied mathematical analysis, shearlets are a multiscale framework which allows efficient encoding of anisotropic features in multivariate problem classes. Originally, shearlets were introduced in 2006 for the analysis and sparse approximation of functions $. They are a natural extension of wavelets, to accommodate the fact that multivariate functions are typically governed by anisotropic features such as edges in images, since wavelets, as isotropic objects, are not capable of capturing such phenomena.$

This article provides a short survey of the concepts, principles and applications of Multirate Filter Banks and Multidimensional Directional Filter Banks.

References

1 2 Ke, Li. "The Correlation between the Wavelet Base Properties and Image Compression". 2007 International Conference on Computational Intelligence and Security Workshops.
↑ Villasenor, John (August 1995). "Wavelet filter evaluation for image compression". IEEE Transactions on Image Processing. 4 (8): 1053–60. Bibcode:1995ITIP....4.1053V. doi:10.1109/83.403412. PMID 18291999.
↑ http://users.ece.utexas.edu/~bevans/students/phd/dong_wei/phd.pdf
↑ Tian, J (1997). "Coifman Wavelet Systems: Approximation, Smoothness, and Computational Algorithms". In M. Bristeau (ed.). Computational Science for the 21st Century. New York: Wiley. pp. 831–840.
1 2 3 4 L. Winger, Lowell (2001). "Biorthogonal nearly coiflet wavelets for image compression". Signal Processing: Image Communication. 16 (9): 859–869. doi:10.1016/S0923-5965(00)00047-3.
↑ "The Bernstein Basis" (PDF). Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable. Geometry and Computing. 1. 2008. pp. 249–260. doi:10.1007/978-3-540-73398-0_11. ISBN 978-3-540-73397-3.
↑ Yang, X (January 2011). "General framework of the construction of biorthogonal wavelets based on Bernstein bases: theory analysis and application in image compression". IET Computer Vision. 5 (1): 50–67. doi:10.1049/iet-cvi.2009.0083.
↑ Liu, Zaide (2007). "Parametrization construction of biorthogonal wavelet filter banks for image coding". Signal, Image and Video Processing. 1: 63–76. doi:10.1007/s11760-007-0001-z. S2CID 46301605.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:1-1] 1 2 Ke, Li. "The Correlation between the Wavelet Base Properties and Image Compression". 2007 International Conference on Computational Intelligence and Security Workshops.

[2] Villasenor, John (August 1995). "Wavelet filter evaluation for image compression". IEEE Transactions on Image Processing. 4 (8): 1053–60. Bibcode:1995ITIP....4.1053V. doi:10.1109/83.403412. PMID 18291999.

[3] ttp://users.ece.utexas.edu/~bevans/students/phd/dong_wei/phd.pdf

[4] Tian, J (1997). "Coifman Wavelet Systems: Approximation, Smoothness, and Computational Algorithms". In M. Bristeau (ed.). Computational Science for the 21st Century. New York: Wiley. pp. 831–840.

[:0-5] 1 2 3 4 L. Winger, Lowell (2001). "Biorthogonal nearly coiflet wavelets for image compression". Signal Processing: Image Communication. 16 (9): 859–869. doi:10.1016/S0923-5965(00)00047-3.

[6] "The Bernstein Basis" (PDF). Pythagorean-Hodograph Curves: Algebra and Geometry Inseparable. Geometry and Computing. 1. 2008. pp. 249–260. doi:10.1007/978-3-540-73398-0_11. ISBN 978-3-540-73397-3.

[7] Yang, X (January 2011). "General framework of the construction of biorthogonal wavelets based on Bernstein bases: theory analysis and application in image compression". IET Computer Vision. 5 (1): 50–67. doi:10.1049/iet-cvi.2009.0083.

[8] Liu, Zaide (2007). "Parametrization construction of biorthogonal wavelet filter banks for image coding". Signal, Image and Video Processing. 1: 63–76. doi:10.1007/s11760-007-0001-z. S2CID 46301605.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]