In geometry, the Brocard circle (or seven-point circle) is a circle derived from a given triangle. It passes through the circumcenter and symmedian of the triangle, and is centered at the midpoint of the line segment joining them (so that this segment is a diameter).
In terms of the side lengths , , and of the given triangle, and the areal coordinates for points inside the triangle (where the -coordinate of a point is the area of the triangle made by that point with the side of length , etc), the Brocard circle consists of the points satisfying the equation [1]
The two Brocard points lie on this circle, as do the vertices of the Brocard triangle. [2] These five points, together with the other two points on the circle (the circumcenter and symmedian), justify the name "seven-point circle".
The Brocard circle is concentric with the first Lemoine circle. [3]
If the triangle is equilateral, the circumcenter and symmedian coincide and therefore the Brocard circle reduces to a single point. [4]
The Brocard circle is named for Henri Brocard, [5] who presented a paper on it to the French Association for the Advancement of Science in Algiers in 1881. [6]
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the centre is called the radius. Usually, the radius is required to be a positive number. A circle with is a degenerate case. This article is about circles in Euclidean geometry, and, in particular, the Euclidean plane, except where otherwise noted.
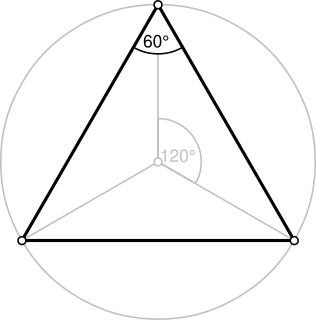
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .
In geometry, bisection is the division of something into two equal or congruent parts, usually by a line, which is then called a bisector. The most often considered types of bisectors are the segment bisector and the angle bisector.
In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
In mathematics and physics, the centroid, also known as geometric center or center of figure, of a plane figure or solid figure is the arithmetic mean position of all the points in the surface of the figure. The same definition extends to any object in n-dimensional Euclidean space.
In Euclidean geometry, a cyclic quadrilateral or inscribed quadrilateral is a quadrilateral whose vertices all lie on a single circle. This circle is called the circumcircle or circumscribed circle, and the vertices are said to be concyclic. The center of the circle and its radius are called the circumcenter and the circumradius respectively. Other names for these quadrilaterals are concyclic quadrilateral and chordal quadrilateral, the latter since the sides of the quadrilateral are chords of the circumcircle. Usually the quadrilateral is assumed to be convex, but there are also crossed cyclic quadrilaterals. The formulas and properties given below are valid in the convex case.
In geometry, the incenter of a triangle is a triangle center, a point defined for any triangle in a way that is independent of the triangle's placement or scale. The incenter may be equivalently defined as the point where the internal angle bisectors of the triangle cross, as the point equidistant from the triangle's sides, as the junction point of the medial axis and innermost point of the grassfire transform of the triangle, and as the center point of the inscribed circle of the triangle.
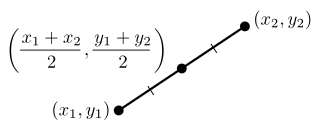
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints, and it is the centroid both of the segment and of the endpoints. It bisects the segment.
In geometry, a set of points are said to be concyclic if they lie on a common circle. All concyclic points are at the same distance from the center of the circle. Three points in the plane that do not all fall on a straight line are concyclic, but four or more such points in the plane are not necessarily concyclic.
In mathematics, a cubic plane curve is a plane algebraic curve C defined by a cubic equation
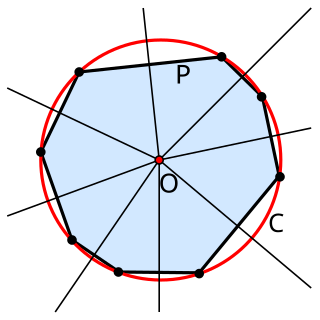
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
In geometry, collinearity of a set of points is the property of their lying on a single line. A set of points with this property is said to be collinear. In greater generality, the term has been used for aligned objects, that is, things being "in a line" or "in a row".
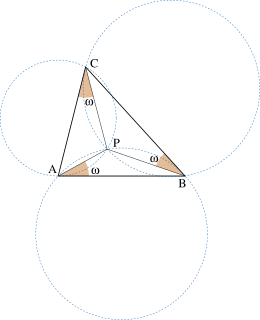
In geometry, Brocard points are special points within a triangle. They are named after Henri Brocard (1845–1922), a French mathematician.
In triangle geometry, the Steiner point is a particular point associated with a triangle. It is a triangle center and it is designated as the center X(99) in Clark Kimberling's Encyclopedia of Triangle Centers. Jakob Steiner (1796–1863), Swiss mathematician, described this point in 1826. The point was given Steiner's name by Joseph Neuberg in 1886.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
In geometry, the orthocentroidal circle of a non-equilateral triangle is the circle that has the triangle's orthocenter and centroid at opposite ends of its diameter. This diameter also contains the triangle's nine-point center and is a subset of the Euler line, which also contains the circumcenter outside the orthocentroidal circle.
In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.
In triangle geometry, the Kiepert conics are two special conics associated with the reference triangle. One of them is a hyperbola, called the Kiepert hyperbola and the other is a parabola, called the Kiepert parabola. The Kiepert conics are defined as follows:
