In graph theory, the girth of an undirected graph is the length of a shortest cycle contained in the graph. If the graph does not contain any cycles, its girth is defined to be infinity. For example, a 4-cycle (square) has girth 4. A grid has girth 4 as well, and a triangular mesh has girth 3. A graph with girth four or more is triangle-free.
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cross each other. Such a drawing is called a plane graph or planar embedding of the graph. A plane graph can be defined as a planar graph with a mapping from every node to a point on a plane, and from every edge to a plane curve on that plane, such that the extreme points of each curve are the points mapped from its end nodes, and all curves are disjoint except on their extreme points.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).
In graph theory, a uniquely colorable graph is a k-chromatic graph that has only one possible (proper) k-coloring up to permutation of the colors. Equivalently, there is only one way to partition its vertices into k independent sets and there is no way to partition them into k − 1 independent sets.

In the mathematical discipline of graph theory, a wheel graph is a graph formed by connecting a single universal vertex to all vertices of a cycle. A wheel graph with n vertices can also be defined as the 1-skeleton of an (n – 1)-gonal pyramid. Some authors write Wn to denote a wheel graph with n vertices ; other authors instead use Wn to denote a wheel graph with n + 1 vertices, which is formed by connecting a single vertex to all vertices of a cycle of length n. The rest of this article uses the former notation.

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.
In the mathematical area of graph theory, the Mycielskian or Mycielski graph of an undirected graph is a larger graph formed from it by a construction of Jan Mycielski (1955). The construction preserves the property of being triangle-free but increases the chromatic number; by applying the construction repeatedly to a triangle-free starting graph, Mycielski showed that there exist triangle-free graphs with arbitrarily large chromatic number.

In the mathematical field of graph theory, the Grötzsch graph is a triangle-free graph with 11 vertices, 20 edges, chromatic number 4, and crossing number 5. It is named after German mathematician Herbert Grötzsch, who used it as an example in connection with his 1959 theorem that planar triangle-free graphs are 3-colorable.
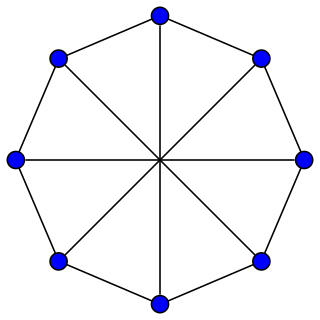
In the mathematical field of graph theory, the Wagner graph is a 3-regular graph with 8 vertices and 12 edges. It is the 8-vertex Möbius ladder graph.

In graph theory, a starSk is the complete bipartite graph K1,k : a tree with one internal node and k leaves. Alternatively, some authors define Sk to be the tree of order k with maximum diameter 2; in which case a star of k > 2 has k − 1 leaves.
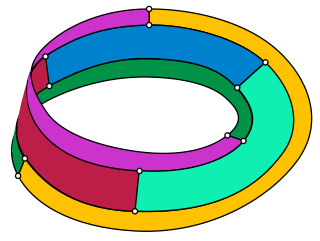
In the mathematical field of graph theory, Tietze's graph is an undirected cubic graph with 12 vertices and 18 edges. It is named after Heinrich Franz Friedrich Tietze, who showed in 1910 that the Möbius strip can be subdivided into six regions that all touch each other – three along the boundary of the strip and three along its center line – and therefore that graphs that are embedded onto the Möbius strip may require six colors. The boundary segments of the regions of Tietze's subdivision form an embedding of Tietze's graph.
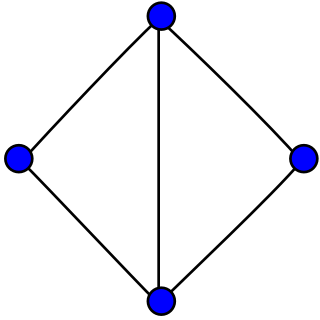
In the mathematical field of graph theory, the diamond graph is a planar, undirected graph with 4 vertices and 5 edges. It consists of a complete graph minus one edge.

In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the dimension-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason (1955), who used it to evaluate the Ramsey number R(3,3,3) = 17.

In the mathematical field of graph theory, the Brinkmann graph is a 4-regular graph with 21 vertices and 42 edges discovered by Gunnar Brinkmann in 1992. It was first published by Brinkmann and Meringer in 1997.

In the mathematical field of graph theory, the bidiakis cube is a 3-regular graph with 12 vertices and 18 edges.

In the mathematical field of graph theory, the friendship graphFn is a planar, undirected graph with 2n + 1 vertices and 3n edges.

In geometric graph theory, a branch of mathematics, a polyhedral graph is the undirected graph formed from the vertices and edges of a convex polyhedron. Alternatively, in purely graph-theoretic terms, the polyhedral graphs are the 3-vertex-connected, planar graphs.

In the mathematical field of graph theory, the Goldner–Harary graph is a simple undirected graph with 11 vertices and 27 edges. It is named after A. Goldner and Frank Harary, who proved in 1975 that it was the smallest non-Hamiltonian maximal planar graph. The same graph had already been given as an example of a non-Hamiltonian simplicial polyhedron by Branko Grünbaum in 1967.

In the mathematical field of graph theory, the triangle graph is a planar undirected graph with 3 vertices and 3 edges, in the form of a triangle.















