In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In discrete mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects are represented by abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges.
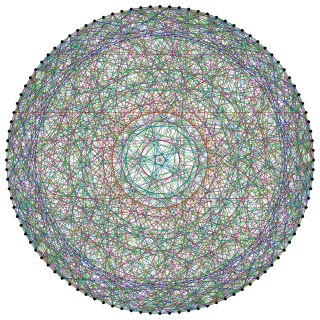
In mathematical graph theory, the Higman–Sims graph is a 22-regular undirected graph with 100 vertices and 1100 edges. It is the unique strongly regular graph srg(100,22,0,6), where no neighboring pair of vertices share a common neighbor and each non-neighboring pair of vertices share six common neighbors. It was first constructed by Mesner (1956) and rediscovered in 1968 by Donald G. Higman and Charles C. Sims as a way to define the Higman–Sims group, a subgroup of index two in the group of automorphisms of the Hoffman–Singleton graph.
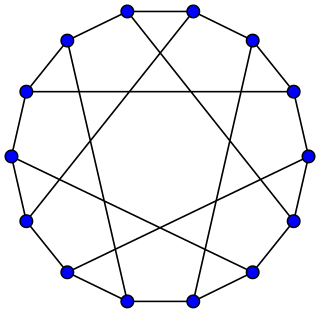
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.

In graph theory, a strongly regular graph (SRG) is a regular graph G = (V, E) with v vertices and degree k such that for some given integers
In mathematics, a two-graph is a set of (unordered) triples chosen from a finite vertex setX, such that every (unordered) quadruple from X contains an even number of triples of the two-graph. A regular two-graph has the property that every pair of vertices lies in the same number of triples of the two-graph. Two-graphs have been studied because of their connection with equiangular lines and, for regular two-graphs, strongly regular graphs, and also finite groups because many regular two-graphs have interesting automorphism groups.

In graph theory, a rook's graph is an undirected graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and there is an edge between any two squares sharing a row (rank) or column (file), the squares that a rook can move between. These graphs can be constructed for chessboards of any rectangular shape. Although rook's graphs have only minor significance in chess lore, they are more important in the abstract mathematics of graphs through their alternative constructions: rook's graphs are the Cartesian product of two complete graphs, and are the line graphs of complete bipartite graphs. The square rook's graphs constitute the two-dimensional Hamming graphs.
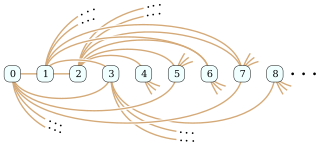
In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann. The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

In the mathematical field of graph theory, the Shrikhande graph is a graph discovered by S. S. Shrikhande in 1959. It is a strongly regular graph with 16 vertices and 48 edges, with each vertex having degree 6. Every pair of nodes has exactly two other neighbors in common, whether or not the pair of nodes is connected.

In the mathematical field of graph theory, the Clebsch graph is either of two complementary graphs on 16 vertices, a 5-regular graph with 40 edges and a 10-regular graph with 80 edges. The 80-edge graph is the dimension-5 halved cube graph; it was called the Clebsch graph name by Seidel (1968) because of its relation to the configuration of 16 lines on the quartic surface discovered in 1868 by the German mathematician Alfred Clebsch. The 40-edge variant is the dimension-5 folded cube graph; it is also known as the Greenwood–Gleason graph after the work of Robert E. Greenwood and Andrew M. Gleason, who used it to evaluate the Ramsey number R(3,3,3) = 17.

In the mathematical field of graph theory, the Brouwer–Haemers graph is a 20-regular undirected graph with 81 vertices and 810 edges. It is a strongly regular graph, a distance-transitive graph, and a Ramanujan graph. Although its construction is folklore, it was named after Andries Brouwer and Willem H. Haemers, who proved its uniqueness as a strongly regular graph.

In the mathematical field of graph theory, the Schläfli graph, named after Ludwig Schläfli, is a 16-regular undirected graph with 27 vertices and 216 edges. It is a strongly regular graph with parameters srg(27, 16, 10, 8).

In mathematics, a near polygon is an incidence geometry introduced by Ernest E. Shult and Arthur Yanushka in 1980. Shult and Yanushka showed the connection between the so-called tetrahedrally closed line-systems in Euclidean spaces and a class of point-line geometries which they called near polygons. These structures generalise the notion of generalized polygon as every generalized 2n-gon is a near 2n-gon of a particular kind. Near polygons were extensively studied and connection between them and dual polar spaces was shown in 1980s and early 1990s. Some sporadic simple groups, for example the Hall-Janko group and the Mathieu groups, act as automorphism groups of near polygons.

The M22 graph, also called the Mesner graph or Witt graph is the unique strongly regular graph with parameters (77, 16, 0, 4). It is constructed from the Steiner system (3, 6, 22) by representing its 77 blocks as vertices and joining two vertices iff they have no terms in common or by deleting a vertex and its neighbors from the Higman–Sims graph.

In graph theory, a locally linear graph is an undirected graph in which every edge belongs to exactly one triangle. Equivalently, for each vertex of the graph, its neighbors are each adjacent to exactly one other neighbor, so the neighbors can be paired up into an induced matching. Locally linear graphs have also been called locally matched graphs. Their triangles form the hyperedges of triangle-free 3-uniform linear hypergraphs and the blocks of certain partial Steiner triple systems, and the locally linear graphs are exactly the Gaifman graphs of these hypergraphs or partial Steiner systems.

In graph theory, Conway's 99-graph problem is an unsolved problem asking whether there exists an undirected graph with 99 vertices, in which each two adjacent vertices have exactly one common neighbor, and in which each two non-adjacent vertices have exactly two common neighbors. Equivalently, every edge should be part of a unique triangle and every non-adjacent pair should be one of the two diagonals of a unique 4-cycle. John Horton Conway offered a $1000 prize for its solution.
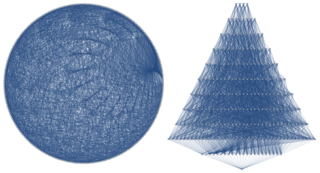
In graph theory, the Berlekamp–Van Lint–Seidel graph is a locally linear strongly regular graph with parameters . This means that it has 243 vertices, 22 edges per vertex, exactly one shared neighbor per pair of adjacent vertices, and exactly two shared neighbors per pair of non-adjacent vertices. It was constructed by Elwyn Berlekamp, J. H. van Lint, and Johan Jacob Seidel as the coset graph of the ternary Golay code.
In graph theory, the Games graph is the largest known locally linear strongly regular graph. Its parameters as a strongly regular graph are (729,112,1,20). This means that it has 729 vertices, and 40824 edges. Each edge is in a unique triangle and each non-adjacent pair of vertices have exactly 20 shared neighbors. It is named after Richard A. Games, who suggested its construction in an unpublished communication and wrote about related constructions.


















