Related Research Articles
In mathematics, an equation is a statement that asserts the equality of two expressions. The word equation and its cognates in other languages may have subtly different meanings; for example, in French an équation is defined as containing one or more variables, while in English any equality is an equation.

In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function.

In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists because most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems.

In mathematics, an eigenfunction of a linear operator D defined on some function space is any non-zero function f in that space that, when acted upon by D, is only multiplied by some scaling factor called an eigenvalue. As an equation, this condition can be written as
In the mathematical subfield of numerical analysis, numerical stability is a generally desirable property of numerical algorithms. The precise definition of stability depends on the context. One is numerical linear algebra and the other is algorithms for solving ordinary and partial differential equations by discrete approximation.

Numerical methods for ordinary differential equations are methods used to find numerical approximations to the solutions of ordinary differential equations (ODEs). Their use is also known as "numerical integration", although this term is sometimes taken to mean the computation of integrals.
In mathematics, a linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form

In mathematics, an integral transform maps a function from its original function space into another function space via integration, where some of the properties of the original function might be more easily characterized and manipulated than in the original function space. The transformed function can generally be mapped back to the original function space using the inverse transform.

A stochastic differential equation (SDE) is a differential equation in which one or more of the terms is a stochastic process, resulting in a solution which is also a stochastic process. SDEs are used to model various phenomena such as unstable stock prices or physical systems subject to thermal fluctuations. Typically, SDEs contain a variable which represents random white noise calculated as the derivative of Brownian motion or the Wiener process. However, other types of random behaviour are possible, such as jump processes.

In mathematics, a differential equation is an equation that relates one or more functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, and the differential equation defines a relationship between the two. Such relations are common, therefore differential equations play a prominent role in many disciplines including engineering, physics, economics, and biology.
Numerical methods for partial differential equations is the branch of numerical analysis that studies the numerical solution of partial differential equations (PDEs).

In mathematics, the method of undetermined coefficients is an approach to finding a particular solution to certain nonhomogeneous ordinary differential equations and recurrence relations. It is closely related to the annihilator method, but instead of using a particular kind of differential operator in order to find the best possible form of the particular solution, a "guess" is made as to the appropriate form, which is then tested by differentiating the resulting equation. For complex equations, the annihilator method or variation of parameters is less time-consuming to perform.
In mathematics, a differential-algebraic system of equations (DAEs) is a system of equations that either contains differential equations and algebraic equations, or is equivalent to such a system. Such systems occur as the general form of differential equations for vector–valued functions x in one independent variable t,
Floquet theory is a branch of the theory of ordinary differential equations relating to the class of solutions to periodic linear differential equations of the form

In mathematics, delay differential equations (DDEs) are a type of differential equation in which the derivative of the unknown function at a certain time is given in terms of the values of the function at previous times. DDEs are also called time-delay systems, systems with aftereffect or dead-time, hereditary systems, equations with deviating argument, or differential-difference equations. They belong to the class of systems with the functional state, i.e. partial differential equations (PDEs) which are infinite dimensional, as opposed to ordinary differential equations (ODEs) having a finite dimensional state vector. Four points may give a possible explanation of the popularity of DDEs:
- Aftereffect is an applied problem: it is well known that, together with the increasing expectations of dynamic performances, engineers need their models to behave more like the real process. Many processes include aftereffect phenomena in their inner dynamics. In addition, actuators, sensors, and communication networks that are now involved in feedback control loops introduce such delays. Finally, besides actual delays, time lags are frequently used to simplify very high order models. Then, the interest for DDEs keeps on growing in all scientific areas and, especially, in control engineering.
- Delay systems are still resistant to many classical controllers: one could think that the simplest approach would consist in replacing them by some finite-dimensional approximations. Unfortunately, ignoring effects which are adequately represented by DDEs is not a general alternative: in the best situation, it leads to the same degree of complexity in the control design. In worst cases, it is potentially disastrous in terms of stability and oscillations.
- Voluntary introduction of delays can benefit the control system.
- In spite of their complexity, DDEs often appear as simple infinite-dimensional models in the very complex area of partial differential equations (PDEs).
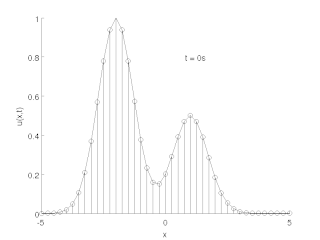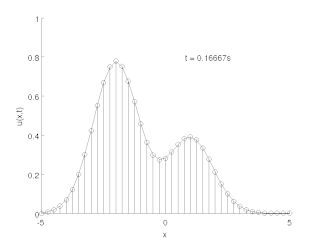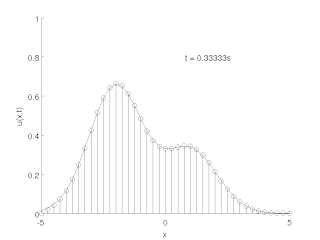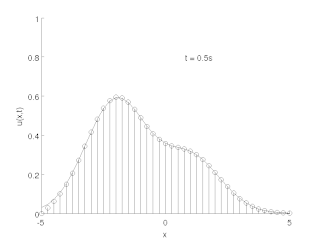
The method of lines is a technique for solving partial differential equations (PDEs) in which all but one dimension is discretized. MOL allows standard, general-purpose methods and software, developed for the numerical integration of ODEs and DAEs, to be used. Many integration routines have been developed over the years in many different programming languages, and some have been published as open source resources.
In mathematics, an ordinary differential equation (ODE) is a differential equation containing one or more functions of one independent variable and the derivatives of those functions. The term ordinary is used in contrast with the term partial differential equation which may be with respect to more than one independent variable.
In mathematics a partial differential algebraic equation (PDAE) set is an incomplete system of partial differential equations that is closed with a set of algebraic equations.
The General Purpose Analog Computer (GPAC) is a mathematical model of analog computers first introduced in 1941 by Claude Shannon. This model consists of circuits where several basic units are interconnected in order to compute some function. The GPAC can be implemented in practice through the use of mechanical devices or analog electronics. Although analog computers have fallen almost into oblivion due to emergence of the digital computer, the GPAC has recently been studied as a way to provide evidence for the physical Church–Turing thesis. This is because the GPAC is also known to model a large class of dynamical systems defined with ordinary differential equations, which appear frequently in the context of physics. In particular it was shown in 2007 that the GPAC is equivalent, in computability terms, to Turing machines, thereby proving the physical Church–Turing thesis for the class of systems modelled by the GPAC. This was recently strengthened to polynomial time equivalence.

Zofia Szmydt was a Polish mathematician working in the areas of differential equations, potential theory and the theory of distributions. She was a winner of the Stefan Banach Prize for mathematics in 1956.