Related Research Articles
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, defined as smooth manifolds with a Riemannian metric. This gives, in particular, local notions of angle, length of curves, surface area and volume. From those, some other global quantities can be derived by integrating local contributions.
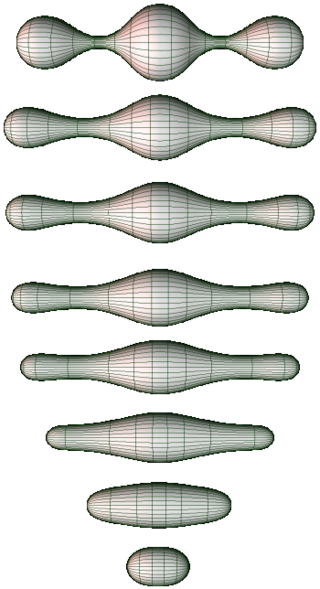
In the mathematical fields of differential geometry and geometric analysis, the Ricci flow, sometimes also referred to as Hamilton's Ricci flow, is a certain partial differential equation for a Riemannian metric. It is often said to be analogous to the diffusion of heat and the heat equation, due to formal similarities in the mathematical structure of the equation. However, it is nonlinear and exhibits many phenomena not present in the study of the heat equation.

Shing-Tung Yau is a Chinese-American mathematician. He is the director of the Yau Mathematical Sciences Center at Tsinghua University and Professor Emeritus at Harvard University. Until 2022, Yau was the William Caspar Graustein Professor of Mathematics at Harvard, at which point he moved to Tsinghua.
In mathematics, Gromov–Hausdorff convergence, named after Mikhail Gromov and Felix Hausdorff, is a notion for convergence of metric spaces which is a generalization of Hausdorff distance.

Eugenio Calabi was an Italian-born American mathematician and the Thomas A. Scott Professor of Mathematics at the University of Pennsylvania, specializing in differential geometry, partial differential equations and their applications.
In the mathematical field of differential geometry, Ricci-flatness is a condition on the curvature of a Riemannian manifold. Ricci-flat manifolds are a special kind of Einstein manifold. In theoretical physics, Ricci-flat Lorentzian manifolds are of fundamental interest, as they are the solutions of Einstein's field equations in a vacuum with vanishing cosmological constant.

Richard Streit Hamilton is an American mathematician who serves as the Davies Professor of Mathematics at Columbia University. He is known for contributions to geometric analysis and partial differential equations. Hamilton is best known for foundational contributions to the theory of the Ricci flow and the development of a corresponding program of techniques and ideas for resolving the Poincaré conjecture and geometrization conjecture in the field of geometric topology. Grigori Perelman built upon Hamilton's results to prove the conjectures, and was awarded a Millennium Prize for his work. However, Perelman declined the award, regarding Hamilton's contribution as being equal to his own.

Mikhael Leonidovich Gromov is a Russian-French mathematician known for his work in geometry, analysis and group theory. He is a permanent member of Institut des Hautes Études Scientifiques in France and a professor of mathematics at New York University.

Richard Melvin Schoen is an American mathematician known for his work in differential geometry and geometric analysis. He is best known for the resolution of the Yamabe problem in 1984.
In the mathematical field of metric geometry, Mikhael Gromov proved a fundamental compactness theorem for sequences of metric spaces. In the special case of Riemannian manifolds, the key assumption of his compactness theorem is automatically satisfied under an assumption on Ricci curvature. These theorems have been widely used in the fields of geometric group theory and Riemannian geometry.

Jeff Cheeger is a mathematician and Silver Professor at the Courant Institute of Mathematical Sciences of New York University. His main interest is differential geometry and its connections with topology and analysis.

Thierry Aubin was a French mathematician who worked at the Centre de Mathématiques de Jussieu, and was a leading expert on Riemannian geometry and non-linear partial differential equations. His fundamental contributions to the theory of the Yamabe equation led, in conjunction with results of Trudinger and Schoen, to a proof of the Yamabe Conjecture: every compact Riemannian manifold can be conformally rescaled to produce a manifold of constant scalar curvature. Along with Yau, he also showed that Kähler manifolds with negative first Chern classes always admit Kähler–Einstein metrics, a result closely related to the Calabi conjecture. The latter result, established by Yau, provides the largest class of known examples of compact Einstein manifolds. Aubin was the first mathematician to propose the Cartan–Hadamard conjecture.
The Geometry Festival is an annual mathematics conference held in the United States.
Frank Morgan is an American mathematician and the Webster Atwell '21 Professor of Mathematics, Emeritus, at Williams College. He is known for contributions to geometric measure theory, minimal surfaces, and differential geometry, including the resolution of the double bubble conjecture. He was vice-president of the American Mathematical Society and the Mathematical Association of America.

Leon Melvyn Simon, born in 1945, is a Leroy P. Steele Prize and Bôcher Prize-winning mathematician, known for deep contributions to the fields of geometric analysis, geometric measure theory, and partial differential equations. He is currently Professor Emeritus in the Mathematics Department at Stanford University.

John William Lott is a professor of Mathematics at the University of California, Berkeley. He is known for contributions to differential geometry.

Carolyn S. Gordon is an American mathematician who is the Benjamin Cheney Professor of Mathematics at Dartmouth College. She is most well known for giving a negative answer to the question "Can you hear the shape of a drum?" in her work with David Webb and Scott A. Wolpert. She is a Chauvenet Prize winner and a 2010 Noether Lecturer.
Guofang Wei is a mathematician in the field of differential geometry. She is a professor at the University of California, Santa Barbara.
In mathematics, the intrinsic flat distance is a notion for distance between two Riemannian manifolds which is a generalization of Federer and Fleming's flat distance between submanifolds and integral currents lying in Euclidean space.

Gerhard Huisken is a German mathematician whose research concerns differential geometry and partial differential equations. He is known for foundational contributions to the theory of the mean curvature flow, including Huisken's monotonicity formula, which is named after him. With Tom Ilmanen, he proved a version of the Riemannian Penrose inequality, which is a special case of the more general Penrose conjecture in general relativity.
References
- 1 2 "Professor Sormani". Google sites. Retrieved Mar 9, 2015.
- ↑ Morgan, Frank (May 28, 2012). "Math now--Commencement can wait". Huffington Post. Retrieved Mar 9, 2015.
- ↑ Christina Sormani at the Mathematics Genealogy Project
- ↑ "Eminent Women in Science Seminar: Christina Sormani, PhD". Rutgers University . Retrieved Mar 9, 2015.
- ↑ "Science Faculty Spotlight: Christina Sormani". CUNY Graduate Center. Retrieved 30 September 2023.
- ↑
- 24th Annual Geometry Festival 2009 in memory of Detlef Gromoll
- ↑ "Association for Women in Mathematics Service Award 2015". Association for Women in Mathematics. Retrieved 30 September 2023.
- ↑ List of Fellows of the American Mathematical Society
- ↑ "Christina Sormani named a 2015 Fellow of the American Mathematical Society". CUNY Graduate Center. Retrieved 30 September 2023.
- ↑ "2024 AWM Fellows". Association for Women in Mathematics. Retrieved 2023-10-26.