
An equilateral triangle is a triangle in which all three sides have the same length, and all three angles are equal. Because of these properties, the equilateral triangle is a regular polygon, occasionally known as the regular triangle. It is the special case of an isosceles triangle by modern definition, creating more special properties.

Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
The Kepler conjecture, named after the 17th-century mathematician and astronomer Johannes Kepler, is a mathematical theorem about sphere packing in three-dimensional Euclidean space. It states that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic close packing and hexagonal close packing arrangements. The density of these arrangements is around 74.05%.

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions or to non-Euclidean spaces such as hyperbolic space.

A Reuleaux triangle is a curved triangle with constant width, the simplest and best known curve of constant width other than the circle. It is formed from the intersection of three circular disks, each having its center on the boundary of the other two. Constant width means that the separation of every two parallel supporting lines is the same, independent of their orientation. Because its width is constant, the Reuleaux triangle is one answer to the question "Other than a circle, what shape can a manhole cover be made so that it cannot fall down through the hole?"

The triaugmented triangular prism, in geometry, is a convex polyhedron with 14 equilateral triangles as its faces. It can be constructed from a triangular prism by attaching equilateral square pyramids to each of its three square faces. The same shape is also called the tetrakis triangular prism, tricapped trigonal prism, tetracaidecadeltahedron, or tetrakaidecadeltahedron; these last names mean a polyhedron with 14 triangular faces. It is an example of a deltahedron, composite polyhedron, and Johnson solid.
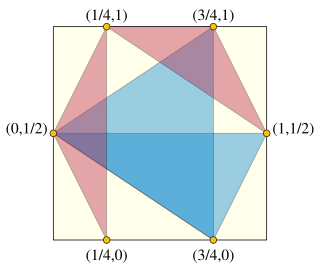
In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points in the plane, avoiding triangles of small area. It is named after Hans Heilbronn, who conjectured that, no matter how points are placed in a given area, the smallest triangle area will be at most inversely proportional to the square of the number of points. His conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown.

In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle.

The circle packing theorem describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles whose interiors are disjoint. The intersection graph of a circle packing is the graph having a vertex for each circle, and an edge for every pair of circles that are tangent. If the circle packing is on the plane, or, equivalently, on the sphere, then its intersection graph is called a coin graph; more generally, intersection graphs of interior-disjoint geometric objects are called tangency graphs or contact graphs. Coin graphs are always connected, simple, and planar. The circle packing theorem states that these are the only requirements for a graph to be a coin graph:

In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.

In geometry, the Tammes problem is a problem in packing a given number of points on the surface of a sphere such that the minimum distance between points is maximized. It is named after the Dutch botanist Pieter Merkus Lambertus Tammes who posed the problem in his 1930 doctoral dissertation on the distribution of pores on pollen grains.
Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack n unit circles into the smallest possible square. Equivalently, the problem is to arrange n points in a unit square aiming to get the greatest minimal separation, dn, between points. To convert between these two formulations of the problem, the square side for unit circles will be L = 2 + 2/dn.
Circle packing in a circle is a two-dimensional packing problem with the objective of packing unit circles into the smallest possible larger circle.
Square packing is a packing problem where the objective is to determine how many congruent squares can be packed into some larger shape, often a square or circle.

Ulam's packing conjecture, named for Stanisław Ulam, is a conjecture about the highest possible packing density of identical convex solids in three-dimensional Euclidean space. The conjecture says that the optimal density for packing congruent spheres is smaller than that for any other convex body. That is, according to the conjecture, the ball is the convex solid which forces the largest fraction of space to remain empty in its optimal packing structure. This conjecture is therefore related to the Kepler conjecture about sphere packing. Since the solution to the Kepler conjecture establishes that identical balls must leave ≈25.95% of the space empty, Ulam's conjecture is equivalent to the statement that no other convex solid forces that much space to be left empty.

In combinatorics, tripod packing is a problem of finding many disjoint tripods in a three-dimensional grid, where a tripod is an infinite polycube, the union of the grid cubes along three positive axis-aligned rays with a shared apex.
In the mathematics of directed graphs, Woodall's conjecture is an unproven relationship between dicuts and dijoins. It was posed by Douglas Woodall in 1976.
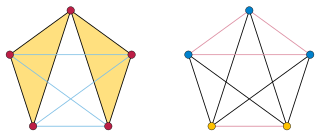
Tuza's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning triangles in undirected graphs.






































