
The travelling salesman problem asks the following question: "Given a list of cities and the distances between each pair of cities, what is the shortest possible route that visits each city exactly once and returns to the origin city?" It is an NP-hard problem in combinatorial optimization, important in theoretical computer science and operations research.
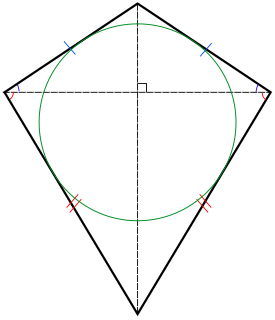
In Euclidean geometry, a kite is a quadrilateral with reflection symmetry across a diagonal. Because of this symmetry, a kite has two equal angles and two pairs of adjacent equal-length sides. Kites are also known as deltoids, but the word deltoid may also refer to a deltoid curve, an unrelated geometric object sometimes studied in connection with quadrilaterals. A kite may also be called a dart, particularly if it is not convex.
A* is a graph traversal and path search algorithm, which is used in many fields of computer science due to its completeness, optimality, and optimal efficiency. One major practical drawback is its space complexity, as it stores all generated nodes in memory. Thus, in practical travel-routing systems, it is generally outperformed by algorithms which can pre-process the graph to attain better performance, as well as memory-bounded approaches; however, A* is still the best solution in many cases.

Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.

In geometry, an isosceles triangle is a triangle that has at least two sides of equal length. Sometimes it is specified as having exactly two sides of equal length, and sometimes as having at least two sides of equal length, the latter version thus including the equilateral triangle as a special case. Examples of isosceles triangles include the isosceles right triangle, the golden triangle, and the faces of bipyramids and certain Catalan solids.
In geometry, the kissing number of a mathematical space is defined as the greatest number of non-overlapping unit spheres that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing in a given space, a kissing number can also be defined for each individual sphere as the number of spheres it touches. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another.
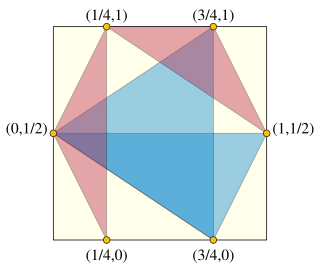
In discrete geometry and discrepancy theory, the Heilbronn triangle problem is a problem of placing points in the plane, avoiding triangles of small area. It is named after Hans Heilbronn, who conjectured that, no matter how points are placed in a given area, the smallest triangle area will be at most inversely proportional to the square of the number of points. His conjecture was proven false, but the asymptotic growth rate of the minimum triangle area remains unknown.

In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle.

A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.
The objective of the Thomson problem is to determine the minimum electrostatic potential energy configuration of n electrons constrained to the surface of a unit sphere that repel each other with a force given by Coulomb's law. The physicist J. J. Thomson posed the problem in 1904 after proposing an atomic model, later called the plum pudding model, based on his knowledge of the existence of negatively charged electrons within neutrally-charged atoms.
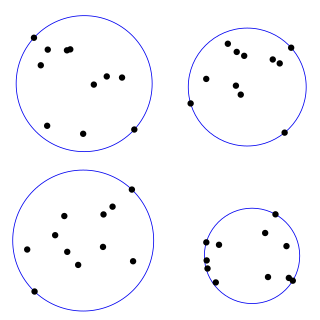
The smallest-circle problem is a mathematical problem of computing the smallest circle that contains all of a given set of points in the Euclidean plane. The corresponding problem in n-dimensional space, the smallest bounding sphere problem, is to compute the smallest n-sphere that contains all of a given set of points. The smallest-circle problem was initially proposed by the English mathematician James Joseph Sylvester in 1857.

In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.
In computational geometry and computer science, the minimum-weight triangulation problem is the problem of finding a triangulation of minimal total edge length. That is, an input polygon or the convex hull of an input point set must be subdivided into triangles that meet edge-to-edge and vertex-to-vertex, in such a way as to minimize the sum of the perimeters of the triangles. The problem is NP-hard for point set inputs, but may be approximated to any desired degree of accuracy. For polygon inputs, it may be solved exactly in polynomial time. The minimum weight triangulation has also sometimes been called the optimal triangulation.
Circle packing in a square is a packing problem in recreational mathematics, where the aim is to pack n unit circles into the smallest possible square. Equivalently, the problem is to arrange n points in a unit square aiming to get the greatest minimal separation, dn, between points. To convert between these two formulations of the problem, the square side for unit circles will be .
Circle packing in a circle is a two-dimensional packing problem with the objective of packing unit circles into the smallest possible larger circle.
Square packing in a square is a packing problem where the objective is to determine how many squares of side one can be packed into a square of side a. If a is an integer, the answer is a2, but the precise, or even asymptotic, amount of wasted space for non-integer a is an open question.

Circle packing in an equilateral triangle is a packing problem in discrete mathematics where the objective is to pack n unit circles into the smallest possible equilateral triangle. Optimal solutions are known for n < 13 and for any triangular number of circles, and conjectures are available for n < 28.
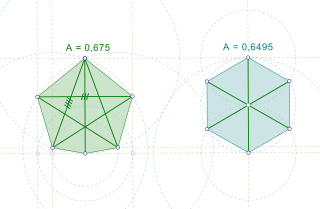
In geometry, the biggest little polygon for a number n is the n-sided polygon that has diameter one and that has the largest area among all diameter-one n-gons. One non-unique solution when n = 4 is a square, and the solution is a regular polygon when n is an odd number, but the solution is irregular otherwise.

In discrete geometry, an opaque set is a system of curves or other set in the plane that blocks all lines of sight across a polygon, circle, or other shape. Opaque sets have also been called barriers, beam detectors, opaque covers, or opaque forests. Opaque sets were introduced by Stefan Mazurkiewicz in 1916, and the problem of minimizing their total length was posed by Frederick Bagemihl in 1959.
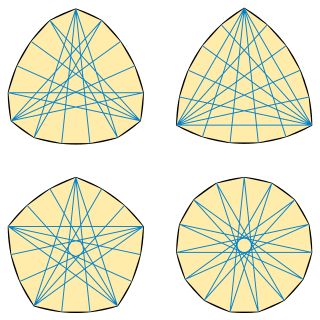
In geometry, a Reinhardt polygon is an equilateral polygon inscribed in a Reuleaux polygon. As in the regular polygons, each vertex of a Reinhardt polygon participates in at least one defining pair of the diameter of the polygon. Reinhardt polygons with sides exist, often with multiple forms, whenever is not a power of two. Among all polygons with sides, the Reinhardt polygons have the largest possible perimeter for their diameter, the largest possible width for their diameter, and the largest possible width for their perimeter. They are named after Karl Reinhardt, who studied them in 1922.


























