Apollonian sphere packing is the three-dimensional equivalent of the Apollonian gasket. The principle of construction is very similar: with any four spheres that are cotangent to each other, it is then possible to construct two more spheres that are cotangent to four of them, resulting in an infinite sphere packing.
The fractal dimension is approximately 2.473946 (±1 in the last digit). [1]
ApolFrac is software for generating and visualization of Apollonian sphere packing. [2]
The Sierpiński triangle, also called the Sierpiński gasket or Sierpiński sieve, is a fractal with the overall shape of an equilateral triangle, subdivided recursively into smaller equilateral triangles. Originally constructed as a curve, this is one of the basic examples of self-similar sets—that is, it is a mathematically generated pattern that is reproducible at any magnification or reduction. It is named after the Polish mathematician Wacław Sierpiński, but appeared as a decorative pattern many centuries before the work of Sierpiński.
In mathematics, the Menger sponge is a fractal curve. It is a three-dimensional generalization of the one-dimensional Cantor set and two-dimensional Sierpinski carpet. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension.
Packing problems are a class of optimization problems in mathematics that involve attempting to pack objects together into containers. The goal is to either pack a single container as densely as possible or pack all objects using as few containers as possible. Many of these problems can be related to real-life packaging, storage and transportation issues. Each packing problem has a dual covering problem, which asks how many of the same objects are required to completely cover every region of the container, where objects are allowed to overlap.
In mathematics, a fractal dimension is a term invoked in the science of geometry to provide a rational statistical index of complexity detail in a pattern. A fractal pattern changes with the scale at which it is measured. It is also a measure of the space-filling capacity of a pattern, and it tells how a fractal scales differently, in a fractal (non-integer) dimension.
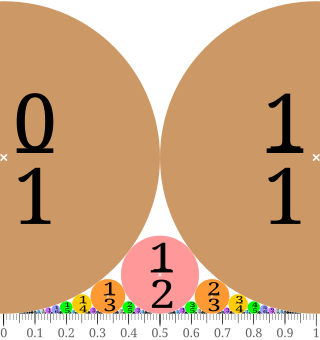
In mathematics, a Ford circle is a circle in the Euclidean plane, in a family of circles that are all tangent to the -axis at rational points. For each rational number , expressed in lowest terms, there is a Ford circle whose center is at the point and whose radius is . It is tangent to the -axis at its bottom point, . The two Ford circles for rational numbers and are tangent circles when and otherwise these two circles are disjoint.
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions or to non-Euclidean spaces such as hyperbolic space.
In geometry, Descartes' theorem states that for every four kissing, or mutually tangent, circles, the radii of the circles satisfy a certain quadratic equation. By solving this equation, one can construct a fourth circle tangent to three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643.
In fractal geometry, the Minkowski–Bouligand dimension, also known as Minkowski dimension or box-counting dimension, is a way of determining the fractal dimension of a set in a Euclidean space , or more generally in a metric space . It is named after the Polish mathematician Hermann Minkowski and the French mathematician Georges Bouligand.
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement. Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek mathematician Apollonius of Perga.
In mathematics, the term chaos game originally referred to a method of creating a fractal, using a polygon and an initial point selected at random inside it. The fractal is created by iteratively creating a sequence of points, starting with the initial random point, in which each point in the sequence is a given fraction of the distance between the previous point and one of the vertices of the polygon; the vertex is chosen at random in each iteration. Repeating this iterative process a large number of times, selecting the vertex at random on each iteration, and throwing out the first few points in the sequence, will often produce a fractal shape. Using a regular triangle and the factor 1/2 will result in the Sierpinski triangle, while creating the proper arrangement with four points and a factor 1/2 will create a display of a "Sierpinski Tetrahedron", the three-dimensional analogue of the Sierpinski triangle. As the number of points is increased to a number N, the arrangement forms a corresponding (N-1)-dimensional Sierpinski Simplex.
In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.
The circles of Apollonius are any of several sets of circles associated with Apollonius of Perga, a renowned Greek geometer. Most of these circles are found in planar Euclidean geometry, but analogs have been defined on other surfaces; for example, counterparts on the surface of a sphere can be defined through stereographic projection.
In mathematics, a surface is a mathematical model of the common concept of a surface. It is a generalization of a plane, but, unlike a plane, it may be curved; this is analogous to a curve generalizing a straight line.
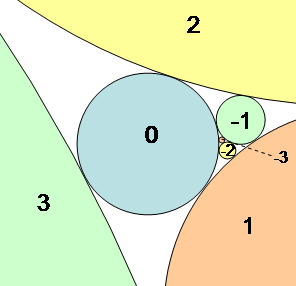
In geometry, Coxeter's loxodromic sequence of tangent circles is an infinite sequence of circles arranged so that any four consecutive circles in the sequence are pairwise mutually tangent. This means that each circle in the sequence is tangent to the three circles that precede it and also to the three circles that follow it.
In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.
An n-flake, polyflake, or Sierpinski n-gon, is a fractal constructed starting from an n-gon. This n-gon is replaced by a flake of smaller n-gons, such that the scaled polygons are placed at the vertices, and sometimes in the center. This process is repeated recursively to result in the fractal. Typically, there is also the restriction that the n-gons must touch yet not overlap.
In fractal geometry, the open set condition (OSC) is a commonly imposed condition on self-similar fractals. In some sense, the condition imposes restrictions on the overlap in a fractal construction. Specifically, given an iterated function system of contractive mappings , the open set condition requires that there exists a nonempty, open set V satisfying two conditions:
In mathematics, the theory of finite sphere packing concerns the question of how a finite number of equally-sized spheres can be most efficiently packed. The question of packing finitely many spheres has only been investigated in detail in recent decades, with much of the groundwork being laid by László Fejes Tóth.
 | This fractal–related article is a stub. You can help Wikipedia by expanding it. |
 | This hyperbolic geometry-related article is a stub. You can help Wikipedia by expanding it. |