Compilation complexity

Last updated April 12, 2024

Compilation complexity is the smallest number of bits required to summarize a input to a function, such that the output of the function can be computed correctly. The notion was particularly studied in voting theory.^[1] Often, a group has to accept a decision, but some of the voters have not arrived yet. It is desired to take the votes of the present voters and summarize them such that, when the other voters arrive, we can determine the winner. The compilation complexity of a voting-rule is the smallest number of bits required for the summary.

An important advantage of low compilation complexity is that it makes it easier to verify voting outcomes. For example, suppose an elections are held in a country of 1,000,000 people, divided into 1000 voting-stations of 1000 voters each. Low compilation complexity lets us summarize the outcome in each voting-station separately, which is relatively easy to verify by double-counting by representatives of the parties. Then, every citizen can verify the final outcome by summing the results from the 1000 voting stations. This verifiability is important so that the public trusts and accepts the voting rule.^[1] Compilation complexity is also algorithmically useful for computing the backward induction winner in Stackelberg voting games.^[2]

Definitions

Let r be a voting rule: a function that takes as input a list of n ranked ballots, representing the preferences of n voters, and returns an outcome. There are some k<n voters whose votes are known. A compilation function is a function f that takes as input a list of k ranked ballots and returns some output such that, given any number u := n-k of additional ranked ballots, the output of r on the entire ballot can be computed exactly.

The compilation complexity of a rule r is the worst-case number of bits in the output of the most efficient compilation function f. This number is typically a function of n (the number of voters), k (the number of known votes) and c (the number of candidates).

A closely related notion is that of equivalence of partial profiles. Suppose there are n voters, of which only k<n have voted. The votes of these k voters are called a partial profile. Given a voting rule r, two partial profiles P and Q on k voters are called r-equivalent if, for any partial profile R, the rule winner on the complete profile P u R is equal to the rule winner on the complete profile Q u R. The relation "r-equivalent" is obviously an equivalence relation, so it partitions the set of profiles on k voters to equivalence classes. We denote by eq(r,k,c) the number of equivalence classes when the voting-rule is r, the number of known votes is k, and the number of candidates is c. The compilation complexity of any rule is the logarithm of the number of equivalence classes, that is, $\lceil \log(eq(r,k,c))\rceil$ .^[1]

Compilation complexity of single-winner voting rules

This section describes bounds on the compilation complexity of some common single-winner voting rules based on ordinal ballots. The results are based on two papers:

Chevaleyre, Lang, Maudet and Ravilli-Abadie^[1] assume that u (= n-k - the number of unknown voters) is unknown, so their results are given as a function of k and c only.
Xia and Conitzer^[2] study also the case that k (the number of known votes) is unknown, and also the case that both u and k are known. For the latter case, lower compilation complexity results are possible. The upper bounds are constructive: they are based on easy-to-compute compilation functions.

Maximum and minimum compilation complexity

The number of equivalence classes for any rule is in $O(\min \left({(c!)}^{k},k^{(c!)}\right))$ . Therefore, the maximum compilation complexity of any voting rule is in $\min \left(k\cdot \log {c!},~c!\cdot \log {k}\right)$ . But there are rules with a much smaller compilation complexity. For example, if there is a sure winner, then the number of equivalence classes is c (the number of possible winners), so the compilation complexity is $\log {c}$ .^[1]

Plurality voting

In plurality voting, any partial profile can be summarized by recording the plurality score of each candidate - the number of times each candidate appears first. Since this number is at most k, the compilation complexity is in $O(c\log {k})$ . Another bound can be attained by counting equivalence classes: the equivalence classes correspond to all vectors of c integers with sum k. Taking the logarithm gives $\Theta (c\log {(1+k/c)}+k\log(1+c/k))$ which is in $O(k+c)$ .^[1]

Borda voting

In Borda voting, any partial profile can be summarized by recording the Borda score of each candidate. Since the Borda score is at most k(c-1), the compilation complexity is at most $(c-1)\cdot \log {(k(c-1))}$ , and there is a matching lower bound, so the complexity is in $\Theta (c\log {kc})$ .^[1] If u is known, then the bound is $\Theta (c\log {\min(kc,uc)})$ .

Voting rules based on weighted majority graph

The weighted majority graph of a voter profile is a directed graph in which the nodes are the candidates, and there is a directed edge from x to y iff a majority of voters prefer x to y. The weight of this edge is the number of voters who prefer x to y. Many rules are based only on the majority graph; the number of equivalence classes of such rules is at most the number of possible weighted majority graphs. This number is denoted by T(k,c) - the number of weighted tournaments on c vertices that can be obtained from k voters. Therefore, the compilation complexity is at most log(T(k,c)). An upper bound on log(T(k,c)) is ${\frac {c(c-1)}{2}}\log(k+1)$ , since it is sufficient to keep, for each pair of candidates x,y, the number of voters who prefer x to y, and this number is between 0 and k.^[1]

For Condorcet-consistent rules based on the unweighted majority graph, such as Copeland or voting tree, there exists some constant q such that the compilation complexity is between $\Omega (c^{2}\log(\min({\frac {k\log c}{qc}}-1,u)))$ and $O(c^{2}\log(\min(k,u))).$ When u is unknown, it is between $\Omega (c^{2}\log({\frac {k}{qm}}-2))$ and $O(c^{2}\log(k)).$ ^[2]

For Condorcet-consistent rules based on the order of pairwise elections, such as ranked pairs or Minimax Condorcet method, there exists some constant q such that the compilation complexity is between $\Omega (c^{2}\log(\min({\frac {k\log c}{qc}}-1,u)))$ and $O(c^{2}\log(\min(k,uc))).$ When u is unknown, it is between $\Omega (c^{2}\log({\frac {k}{qm}}-2))$ and $O(c^{2}\log(k)).$ ^[2]

For Condorcet-consistent rules based on the weighted majority graph, when u is unknown, the compilation complexity is between $\Omega (\min(c^{2}\log k,cu\log {u}))$ and $O(c^{2}\log(k)).$ ^[1]

Voting rules with runoff

The compilation complexity of two-round voting (plurality with runoff) is in $\Theta (c^{2}\log {k})$ . Note that this is higher than the compilation complexity of Borda voting, though the communication complexity of two-round voting is lower than that of Borda voting.^[3] When u is known, the bound is $\Theta (c^{2}\log {\min(u,k)})$ .

The compilation complexity of Single transferable vote is in $\Omega \left(2^{c}\log(1+{\frac {k}{2^{c}}})+k\log(1+{\frac {2^{c}}{k}})\right)$ and in $O\left(c2^{c}\log(1+{\frac {k}{2^{c}}})+kc\log(1+{\frac {2^{c}}{k}})\right)$ . ^[1]

Bucklin's rule

For the Bucklin voting rule, if min(k,u) ≥ m ≥ 12, the compilation complexity is in $\Theta (c^{2}\log {\min(k,u)})$ ; when u is unknown it is $\Theta (c^{2}\log {k})$ .^[2]

Compilation complexity of multi-winner voting rules

Karia and Lang^[4] study the compilation complexity of several multiwinner voting rules, with either ranked ballots or approval ballots. For example:

For Single non-transferable vote, the complexity is in $\Theta (c\log {(1+k/c)}+k\log(1+c/k))$ .
For Borda, the complexity is in $\Theta (c\log {kc})$ .

Related Research Articles

<span class="mw-page-title-main">Rutherford scattering</span> Elastic scattering of charged particles by the Coulomb force

In particle physics, Rutherford scattering is the elastic scattering of charged particles by the Coulomb interaction. It is a physical phenomenon explained by Ernest Rutherford in 1911 that led to the development of the planetary Rutherford model of the atom and eventually the Bohr model. Rutherford scattering was first referred to as Coulomb scattering because it relies only upon the static electric (Coulomb) potential, and the minimum distance between particles is set entirely by this potential. The classical Rutherford scattering process of alpha particles against gold nuclei is an example of "elastic scattering" because neither the alpha particles nor the gold nuclei are internally excited. The Rutherford formula further neglects the recoil kinetic energy of the massive target nucleus.

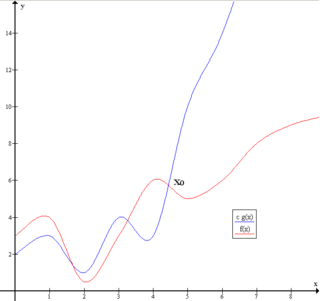
Big <i>O</i> notation Describes limiting behavior of a function

Big O notation is a mathematical notation that describes the limiting behavior of a function when the argument tends towards a particular value or infinity. Big O is a member of a family of notations invented by German mathematicians Paul Bachmann, Edmund Landau, and others, collectively called Bachmann–Landau notation or asymptotic notation. The letter O was chosen by Bachmann to stand for Ordnung, meaning the order of approximation.

In statistics, the Lehmann–Scheffé theorem is a prominent statement, tying together the ideas of completeness, sufficiency, uniqueness, and best unbiased estimation. The theorem states that any estimator that is unbiased for a given unknown quantity and that depends on the data only through a complete, sufficient statistic is the unique best unbiased estimator of that quantity. The Lehmann–Scheffé theorem is named after Erich Leo Lehmann and Henry Scheffé, given their two early papers.

A randomized algorithm is an algorithm that employs a degree of randomness as part of its logic or procedure. The algorithm typically uses uniformly random bits as an auxiliary input to guide its behavior, in the hope of achieving good performance in the "average case" over all possible choices of random determined by the random bits; thus either the running time, or the output are random variables.

In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular arc. It can be uniform, with a constant rate of rotation and constant tangential speed, or non-uniform with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves the circular motion of its parts. The equations of motion describe the movement of the center of mass of a body, which remains at a constant distance from the axis of rotation. In circular motion, the distance between the body and a fixed point on its surface remains the same, i.e., the body is assumed rigid.

In mathematical statistics, the Fisher information is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X. Formally, it is the variance of the score, or the expected value of the observed information.

In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of L^p-norms of the function together with its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, i.e. a Banach space. Intuitively, a Sobolev space is a space of functions possessing sufficiently many derivatives for some application domain, such as partial differential equations, and equipped with a norm that measures both the size and regularity of a function.

In computer science, a disjoint-set data structure, also called a union–find data structure or merge–find set, is a data structure that stores a collection of disjoint (non-overlapping) sets. Equivalently, it stores a partition of a set into disjoint subsets. It provides operations for adding new sets, merging sets, and finding a representative member of a set. The last operation makes it possible to find out efficiently if any two elements are in the same or different sets.

The Schönhage–Strassen algorithm is an asymptotically fast multiplication algorithm for large integers, published by Arnold Schönhage and Volker Strassen in 1971. It works by recursively applying fast Fourier transform (FFT) over the integers modulo 2ⁿ+1. The run-time bit complexity to multiply two $n$ -digit numbers using the algorithm is $in big O notation .$

In statistics a minimum-variance unbiased estimator (MVUE) or uniformly minimum-variance unbiased estimator (UMVUE) is an unbiased estimator that has lower variance than any other unbiased estimator for all possible values of the parameter.

In statistics, the score test assesses constraints on statistical parameters based on the gradient of the likelihood function—known as the score—evaluated at the hypothesized parameter value under the null hypothesis. Intuitively, if the restricted estimator is near the maximum of the likelihood function, the score should not differ from zero by more than sampling error. While the finite sample distributions of score tests are generally unknown, they have an asymptotic χ²-distribution under the null hypothesis as first proved by C. R. Rao in 1948, a fact that can be used to determine statistical significance.

In statistics, the Bayesian information criterion (BIC) or Schwarz information criterion is a criterion for model selection among a finite set of models; models with lower BIC are generally preferred. It is based, in part, on the likelihood function and it is closely related to the Akaike information criterion (AIC).

In mathematics, the axis–angle representation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector $e$ indicating the direction (geometry) of an axis of rotation, and an angle of rotation $θ$ describing the magnitude and sense of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector $e$ rooted at the origin because the magnitude of $e$ is constrained. For example, the elevation and azimuth angles of $e$ suffice to locate it in any particular Cartesian coordinate frame.

<span class="mw-page-title-main">Vibrations of a circular membrane</span> Equations of waves in a drumhead-like disc

A two-dimensional elastic membrane under tension can support transverse vibrations. The properties of an idealized drumhead can be modeled by the vibrations of a circular membrane of uniform thickness, attached to a rigid frame. Due to the phenomenon of resonance, at certain vibration frequencies, its resonant frequencies, the membrane can store vibrational energy, the surface moving in a characteristic pattern of standing waves. This is called a normal mode. A membrane has an infinite number of these normal modes, starting with a lowest frequency one called the fundamental mode.

In mathematics, potential flow around a circular cylinder is a classical solution for the flow of an inviscid, incompressible fluid around a cylinder that is transverse to the flow. Far from the cylinder, the flow is unidirectional and uniform. The flow has no vorticity and thus the velocity field is irrotational and can be modeled as a potential flow. Unlike a real fluid, this solution indicates a net zero drag on the body, a result known as d'Alembert's paradox.

In quantum computing, the quantum phase estimation algorithm is a quantum algorithm to estimate the phase corresponding to an eigenvalue of a given unitary operator. Because the eigenvalues of a unitary operator always have unit modulus, they are characterized by their phase, and therefore the algorithm can be equivalently described as retrieving either the phase or the eigenvalue itself. The algorithm was initially introduced by Alexei Kitaev in 1995.

In coding theory, generalized minimum-distance (GMD) decoding provides an efficient algorithm for decoding concatenated codes, which is based on using an errors-and-erasures decoder for the outer code.

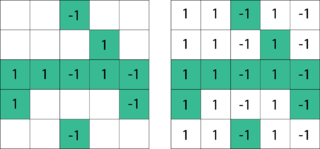
<span class="mw-page-title-main">Matrix completion</span>

Matrix completion is the task of filling in the missing entries of a partially observed matrix, which is equivalent to performing data imputation in statistics. A wide range of datasets are naturally organized in matrix form. One example is the movie-ratings matrix, as appears in the Netflix problem: Given a ratings matrix in which each entry $represents the rating of movie by customer, if customer has watched movie and is otherwise missing, we would like to predict the remaining entries in order to make good recommendations to customers on what to watch next. Another example is the document-term matrix: The frequencies of words used in a collection of documents can be represented as a matrix, where each entry corresponds to the number of times the associated term appears in the indicated document.$

In mathematics, and in particular in mathematical analysis, the Gagliardo–Nirenberg interpolation inequality is a result in the theory of Sobolev spaces that relates the $-norms of different weak derivatives of a function through an interpolation inequality. The theorem is of particular importance in the framework of elliptic partial differential equations and was originally formulated by Emilio Gagliardo and Louis Nirenberg in 1958. The Gagliardo-Nirenberg inequality has found numerous applications in the investigation of nonlinear partial differential equations, and has been generalized to fractional Sobolev spaces by Haim Brezis and Petru Mironescu in the late 2010s.$

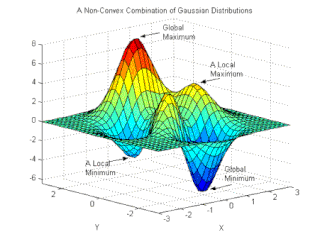
Stochastic gradient Langevin dynamics (SGLD) is an optimization and sampling technique composed of characteristics from Stochastic gradient descent, a Robbins–Monro optimization algorithm, and Langevin dynamics, a mathematical extension of molecular dynamics models. Like stochastic gradient descent, SGLD is an iterative optimization algorithm which uses minibatching to create a stochastic gradient estimator, as used in SGD to optimize a differentiable objective function. Unlike traditional SGD, SGLD can be used for Bayesian learning as a sampling method. SGLD may be viewed as Langevin dynamics applied to posterior distributions, but the key difference is that the likelihood gradient terms are minibatched, like in SGD. SGLD, like Langevin dynamics, produces samples from a posterior distribution of parameters based on available data. First described by Welling and Teh in 2011, the method has applications in many contexts which require optimization, and is most notably applied in machine learning problems.

References

1 2 3 4 5 6 7 8 9 10 11 Chevaleyre, Yann; Lang, Jérôme; Maudet, Nicolas; Ravilly-Abadie, Guillaume (2009-07-11). "Compiling the votes of a subelectorate". Proceedings of the 21st International Joint Conference on Artificial Intelligence. IJCAI'09. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.: 97–102.
1 2 3 4 5 Xia, Lirong; Conitzer, Vincent (2010-07-04). "Compilation Complexity of Common Voting Rules". Proceedings of the AAAI Conference on Artificial Intelligence. 24 (1): 915–920. doi: 10.1609/aaai.v24i1.7627 . ISSN 2374-3468.
1 2 Conitzer, Vincent; Sandholm, Tuomas (2005-06-05). "Communication complexity of common voting rules". Proceedings of the 6th ACM conference on Electronic commerce. EC '05. New York, NY, USA: Association for Computing Machinery. pp. 78–87. doi:10.1145/1064009.1064018. ISBN 978-1-59593-049-1.
↑ Karia, Neel; Lang, Jérôme (2021-05-18). "Compilation Complexity of Multi-Winner Voting Rules (Student Abstract)". Proceedings of the AAAI Conference on Artificial Intelligence. 35 (18): 15809–15810. doi: 10.1609/aaai.v35i18.17901 . ISSN 2374-3468.

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 3 4 5 6 7 8 9 10 11 Chevaleyre, Yann; Lang, Jérôme; Maudet, Nicolas; Ravilly-Abadie, Guillaume (2009-07-11). "Compiling the votes of a subelectorate". Proceedings of the 21st International Joint Conference on Artificial Intelligence. IJCAI'09. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.: 97–102.

[:2-2] 1 2 3 4 5 Xia, Lirong; Conitzer, Vincent (2010-07-04). "Compilation Complexity of Common Voting Rules". Proceedings of the AAAI Conference on Artificial Intelligence. 24 (1): 915–920. doi: 10.1609/aaai.v24i1.7627 . ISSN 2374-3468.

[:1-3] 1 2 Conitzer, Vincent; Sandholm, Tuomas (2005-06-05). "Communication complexity of common voting rules". Proceedings of the 6th ACM conference on Electronic commerce. EC '05. New York, NY, USA: Association for Computing Machinery. pp. 78–87. doi:10.1145/1064009.1064018. ISBN 978-1-59593-049-1.

[4] Karia, Neel; Lang, Jérôme (2021-05-18). "Compilation Complexity of Multi-Winner Voting Rules (Student Abstract)". Proceedings of the AAAI Conference on Artificial Intelligence. 35 (18): 15809–15810. doi: 10.1609/aaai.v35i18.17901 . ISSN 2374-3468.

[1]

[2]

[3]

[4]