
The Copeland or Llull method is a ranked-choice voting system based on counting each candidate's pairwise wins and losses.
The Gibbard–Satterthwaite theorem is a theorem in voting theory. It was first conjectured by the philosopher Michael Dummett and the mathematician Robin Farquharson in 1961 and then proved independently by the philosopher Allan Gibbard in 1973 and economist Mark Satterthwaite in 1975. It deals with deterministic ordinal electoral systems that choose a single winner, and shows that for every voting rule of this form, at least one of the following three things must hold:
- The rule is dictatorial, i.e. there exists a distinguished voter who can choose the winner; or
- The rule limits the possible outcomes to two alternatives only; or
- The rule is not straightforward, i.e. there is no single always-best strategy.

In graph theory, a tournament is a directed graph with exactly one edge between each two vertices, in one of the two possible directions. Equivalently, a tournament is an orientation of an undirected complete graph. The name tournament comes from interpreting the graph as the outcome of a round-robin tournament, a game where each player is paired against every other exactly once. In a tournament, the vertices represent the players, and the edges between players point from the winner to the loser.

Positional voting is a ranked voting electoral system in which the options or candidates receive points based on their rank position on each ballot and the one with the most points overall wins. The lower-ranked preference in any adjacent pair is generally of less value than the higher-ranked one. Although it may sometimes be weighted the same, it is never worth more. A valid progression of points or weightings may be chosen at will or it may form a mathematical sequence such as an arithmetic progression, a geometric one or a harmonic one. The set of weightings employed in an election heavily influences the rank ordering of the candidates. The steeper the initial decline in preference values with descending rank, the more polarised and less consensual the positional voting system becomes.

The Kemeny–Young method is an electoral system that uses ranked ballots and pairwise comparison counts to identify the most popular choices in an election. It is a Condorcet method because if there is a Condorcet winner, it will always be ranked as the most popular choice.
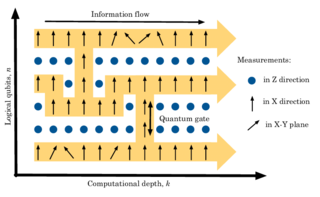
The one-way quantum computer, also known as measurement-based quantum computer (MBQC), is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.
Quantum complexity theory is the subfield of computational complexity theory that deals with complexity classes defined using quantum computers, a computational model based on quantum mechanics. It studies the hardness of computational problems in relation to these complexity classes, as well as the relationship between quantum complexity classes and classical complexity classes.
In graph theory, the Lovász number of a graph is a real number that is an upper bound on the Shannon capacity of the graph. It is also known as Lovász theta function and is commonly denoted by , using a script form of the Greek letter theta to contrast with the upright theta used for Shannon capacity. This quantity was first introduced by László Lovász in his 1979 paper On the Shannon Capacity of a Graph.

Proportional approval voting (PAV) is a proportional electoral system for multiwinner elections. It is a multiwinner approval method that extends the highest averages method of apportionment commonly used to calculate apportionments for party-list proportional representation. However, PAV allows voters to support only the candidates they approve of, rather than being forced to approve or reject all candidates on a given party list.

Sequential proportional approval voting (SPAV) or reweighted approval voting (RAV) is an electoral system that extends the concept of approval voting to a multiple winner election. It is a simplified version of proportional approval voting. It is a special case of Thiele's voting rules, proposed by Danish statistician Thorvald N. Thiele in the early 1900s. It was used in Sweden from 1909 to 1921, when it was replaced by a cruder "party-list" style system as it was easier to calculate, and is still used for some local elections.
Computational social choice is a field at the intersection of social choice theory, theoretical computer science, and the analysis of multi-agent systems. It consists of the analysis of problems arising from the aggregation of preferences of a group of agents from a computational perspective. In particular, computational social choice is concerned with the efficient computation of outcomes of voting rules, with the computational complexity of various forms of manipulation, and issues arising from the problem of representing and eliciting preferences in combinatorial settings.
In the fields of mechanism design and social choice theory, Gibbard's theorem is a result proven by philosopher Allan Gibbard in 1973. It states that for any deterministic process of collective decision, at least one of the following three properties must hold:
- The process is dictatorial, i.e. there is a single voter whose vote chooses the outcome.
- The process limits the possible outcomes to two options only.
- The process is not straightforward; the optimal ballot for a voter "requires strategic voting", i.e. it depends on their beliefs about other voters' ballots.

Justified representation (JR) is a criterion of fairness in multiwinner approval voting. It can be seen as an adaptation of the proportional representation criterion to approval voting.

Multiwinner approval voting, sometimes also called approval-based committee (ABC) voting, refers to a family of multi-winner electoral systems that use approval ballots. Each voter may select ("approve") any number of candidates, and multiple candidates are elected.

Multiwinner, at-large, or committeevoting refers to electoral systems that elect several candidates at once. Such methods can be used to elect parliaments or committees.

Phragmén's voting rules are rules for multiwinner voting. They allow voters to vote for individual candidates rather than parties, but still guarantee proportional representation. They were published by Lars Edvard Phragmén in French and Swedish between 1893 and 1899, and translated to English by Svante Janson in 2016.

The method of equal shares is a proportional method of counting ballots that applies to participatory budgeting, to committee elections, and to simultaneous public decisions. It can be used when the voters vote via approval ballots, ranked ballots or cardinal ballots. It works by dividing the available budget into equal parts that are assigned to each voter. The method is only allowed to use the budget share of a voter to implement projects that the voter voted for. It then repeatedly finds projects that can be afforded using the budget shares of the supporting voters. In contexts other than participatory budgeting, the method works by equally dividing an abstract budget of "voting power".
Multi-issue voting is a setting in which several issues have to be decided by voting. Multi-issue voting raises several considerations, that are not relevant in single-issue voting.
In cooperative game theory, the nucleolus of a cooperative game is the solution that maximizes the smallest excess of a coalition. Subject to that, the nucleolus satisfies the second-smallest excess; and so on, in the leximin order. The nucleolus was introduced by David Schmeidler.
Fully proportional representation(FPR) is a property of multiwinner voting systems. It extends the property of proportional representation (PR) by requiring that the representation be based on the entire preferences of the voters, rather than on their first choice. Moreover, the requirement combines PR with the requirement of accountability - each voter knows exactly which elected candidate represents him, and each candidate knows exactly which voters he represents.











