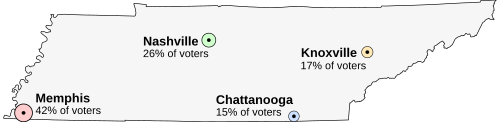
A Condorcet method is an election method that elects the candidate who wins a majority of the vote in every head-to-head election against each of the other candidates, whenever there is such a candidate. A candidate with this property, the pairwise champion or beats-all winner, is formally called the Condorcet winner. The head-to-head elections need not be done separately; a voter's choice within any given pair can be determined from the ranking.

Copeland's method, also called Llull's method or round-robin voting, is a ranked-choice voting system based on scoring pairwise wins and losses.
The Smith set, also known as the top cycle, is a concept from the theory of electoral systems that generalizes the Condorcet winner to cases where no such winner exists, by allowing cycles of candidates to be treated jointly as if they were a single Condorcet winner. Named after John H. Smith, the Smith set is the smallest non-empty set of candidates in a particular election, such that each member defeats every candidate outside the set in a pairwise election. The Smith set provides one standard of optimal choice for an election outcome. Voting systems that always elect a candidate from the Smith set pass the Smith criterion.
Ranked pairs, sometimes called the Tideman method, is a tournament-style system of ranked-choice voting first proposed by Nicolaus Tideman in 1987.
The Schulze method is a single winner ranked-choice voting rule developed by Markus Schulze. It is also known as the beatpath method. The Schulze method is a Condorcet method, which means it will elect a majority-choice candidate if one exists; in other words, if most people rank A above B, A will defeat B.
In an election, a candidate is called a Condorcet, beats-all, or majority-rule winner if a majority of voters would support them in a race against any other candidate. Such a candidate is also called an undefeated or tournament champion. Voting systems where a majority-rule winner will always win the election are said to satisfy the majority-rule principle, also known as the Condorcet criterion. Condorcet voting methods extend majority rule to elections with more than one candidate.
The Smith criterion is a voting system criterion that formalizes the concept of a majority rule. A voting system satisfies the Smith criterion if it always elects a candidate from the Smith set, which generalizes the idea of a "Condorcet winner" to cases where there may be cycles or ties, by allowing for several who together can be thought of as being "Condorcet winners." A Smith method will always elect a candidate from the Smith set.
The participation criterion, also called vote or population monotonicity, is a voting system criterion that says that a candidate should never lose an election because they have "too much support." It says that adding voters who support A over B should not cause A to lose the election to B.
A voting system satisfies join-consistency if combining two sets of votes, both electing A over B, always results in a combined electorate that ranks A over B. It is a stronger form of the participation criterion, which only requires join-consistency when one of the sets of votes unanimously prefers A over B.
The mutual majority criterion is a criterion for evaluating electoral system. It requires that whenever a majority of voters prefer a group of candidates above all others, someone from that group must win.
In single-winner voting system theory, the Condorcet loser criterion (CLC) is a measure for differentiating voting systems. It implies the majority loser criterion but does not imply the Condorcet winner criterion.
Reversal symmetry is a voting system criterion which requires that if candidate A is the unique winner, and each voter's individual preferences are inverted, then A must not be elected. Methods that satisfy reversal symmetry include Borda count, ranked pairs, Kemeny–Young method, and Schulze method. Methods that fail include Bucklin voting, instant-runoff voting and Condorcet methods that fail the Condorcet loser criterion such as Minimax.
The Kemeny–Young method is an electoral system that uses ranked ballots and pairwise comparison counts to identify the most popular choices in an election. It is a Condorcet method because if there is a Condorcet winner, it will always be ranked as the most popular choice.
In voting systems theory, the independence of clones criterion measures an election method's robustness to strategic nomination. Nicolaus Tideman was the first to formulate this criterion, which states that the winner must not change due to the addition of a non-winning candidate who is similar to a candidate already present. It is a relative criterion: it states how changing an election should or shouldn't affect the outcome.

The term ranked voting, also known as preferential voting or ranked-choice voting, pertains to any voting system where voters indicate a rank to order candidates or options—in a sequence from first, second, third, and onwards—on their ballots. Ranked voting systems vary based on the ballot marking process, how preferences are tabulated and counted, the number of seats available for election, and whether voters are allowed to rank candidates equally.
Maximal lotteries are a probabilistic voting method and tournament solution, first proposed by the French mathematician and social scientist Germain Kreweras in 1965, and popularized by Peter Fishburn. The method uses ranked ballots and returns the probability distribution of candidates that is preferred by a majority of voters to any other.
The later-no-help criterion is a voting system criterion formulated by Douglas Woodall. The criterion is satisfied if, in any election, a voter giving an additional ranking or positive rating to a less-preferred candidate can not cause a more-preferred candidate to win. Voting systems that fail the later-no-help criterion are vulnerable to the tactical voting strategy called mischief voting, which can deny victory to a sincere Condorcet winner.
A major branch of social choice theory is devoted to the comparison of electoral systems, otherwise known as social choice functions. Viewed from the perspective of political science, electoral systems are rules for conducting elections and determining winners from the ballots cast. From the perspective of economics, mathematics, and philosophy, a social choice function is a mathematical function that determines how a society should make choices, given a collection of individual preferences.
Multiwinner voting, also called committee voting or committee elections, is an electoral system in which multiple candidates are elected. The number of elected candidates is usually fixed in advance. For example, it can be the number of seats in a country's parliament, or the required number of members in a committee.
Round-robin voting refers to a set of ranked voting systems that elect winners by comparing all candidates in a round-robin tournament. Every candidate is matched up against every other candidate, where their point total is equal to the number of votes they receive; the method then selects a winner based on the results of these paired matchups.