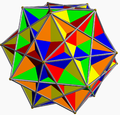
Compound of five cubes

Compound of five cubes
(Animation, 3D model)
Type	Regular compound
Coxeter symbol	2{5,3}[5{4,3}] [1] [2]
Stellation core	rhombic triacontahedron
Convex hull	Dodecahedron
Index	UC9
Polyhedra	5 cubes
Faces	30 squares (visible as 360 triangles)
Edges	60
Vertices	20
Dual	Compound of five octahedra
Symmetry group	icosahedral (Ih)
Subgroup restricting to one constituent	pyritohedral (Th)

Model by Max Brückner (1900)

Model with dodecahedron

The compound of five cubes is one of the five regular polyhedral compounds. It was first described by Edmund Hess in 1876.

Its vertices are those of a regular dodecahedron. Its edges form pentagrams, which are the stellations of the pentagonal faces of the dodecahedron.

It is one of the stellations of the rhombic triacontahedron. Its dual is the compound of five octahedra. It has icosahedral symmetry (I_h).

The compound of five cubes can also be known as a rhombihedron.

Geometry

The compound is a faceting of the dodecahedron. Each cube represents a selection of 8 of the 20 vertices of the dodecahedron.

	Views from 2-fold, 5-fold and 3-fold symmetry axis

If the shape is considered as a union of five cubes yielding a simple nonconvex solid without self-intersecting surfaces, then it has 360 faces (all triangles), 182 vertices (60 with degree 3, 30 with degree 4, 12 with degree 5, 60 with degree 8, and 20 with degree 12), and 540 edges, yielding an Euler characteristic of 182 − 540 + 360 = 2.

Edge arrangement

Its convex hull is a regular dodecahedron. ^[3] It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron, the great ditrigonal icosidodecahedron, and the ditrigonal dodecadodecahedron. With these, it can form polyhedral compounds that can also be considered as degenerate uniform star polyhedra; the small complex rhombicosidodecahedron, great complex rhombicosidodecahedron and complex rhombidodecadodecahedron.

Small ditrigonal icosidodecahedron	Great ditrigonal icosidodecahedron	Ditrigonal dodecadodecahedron
Dodecahedron (convex hull)	Compound of five cubes	As a spherical tiling

The compound of ten tetrahedra can be formed by taking each of these five cubes and replacing them with the two tetrahedra of the stella octangula (which share the same vertex arrangement of a cube).

As a stellation

This compound can be formed as a stellation of the rhombic triacontahedron.
The 30 rhombic faces exist in the planes of the 5 cubes.

Stellation facets The yellow area corresponds to one cube face.

Illustrations by Edmund Hess (1876) In the top right the same figure as on the left. In the bottom right a stellation diagram of the compound of five octahedra.

See also

Transition to compound of four cubes

Compound of five octahedra Compound of three cubes Compound of four cubes Compound of six cubes Uniform polyhedron compound

Footnotes

1. Coxeter 1973, pp. 49-50.
2. Coxeter 1973, p 98.
3. Cromwell 1997, p.  360–361. sfnp error: no target: CITEREFCromwell_1997 (help)

References

• Cromwell, Peter R. (1997), Polyhedra, Cambridge, p. 360.
• Harman, Michael G. (c. 1974), Polyhedral Compounds, unpublished manuscript.
• Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society , 79 (3): 447–457, Bibcode:1976MPCPS..79..447S, doi:10.1017/S0305004100052440, MR   0397554, S2CID   123279687 .
• Cundy, H. and Rollett, A. "Five Cubes in a Dodecahedron." §3.10.6 in Mathematical Models , 3rd ed. Stradbroke, England: Tarquin Pub., pp. 135–136, 1989.
• Coxeter, H. S. M. (1973), Regular Polytopes (3rd ed.), Dover edition, ISBN   0-486-61480-8 , 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
• McCooey, Robert. "Uniform Polyhedron Compounds". Hedron Dude. Retrieved 24 June 2025.

External links

• MathWorld: Cube 5-Compound
  • MathWorld: Rhombic Triacontahedron Stellations
• George Hart: Compounds of Cubes
• Steven Dutch: Uniform Polyhedra and Their Duals
• Klitzing, Richard. "3D compound".