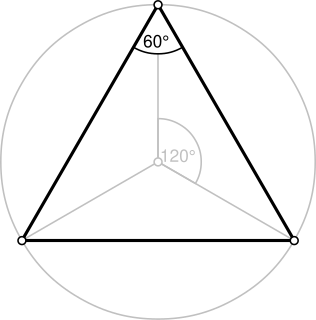
A triangle is a polygon with three edges and three vertices. It is one of the basic shapes in geometry. A triangle with vertices A, B, and C is denoted .

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the incircle or inscribed circle of a triangle is the largest circle contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In mathematics and physics, the centroid or geometric center of a plane figure is the arithmetic mean position of all the points in the figure. Informally, it is the point at which a cutout of the shape could be perfectly balanced on the tip of a pin.

In geometry, the Euler line, named after Leonhard Euler, is a line determined from any triangle that is not equilateral. It is a central line of the triangle, and it passes through several important points determined from the triangle, including the orthocenter, the circumcenter, the centroid, the Exeter point and the center of the nine-point circle of the triangle.

In the geometry of triangles, the incircle and nine-point circle of a triangle are internally tangent to each other at the Feuerbach point of the triangle. The Feuerbach point is a triangle center, meaning that its definition does not depend on the placement and scale of the triangle. It is listed as X(11) in Clark Kimberling's Encyclopedia of Triangle Centers, and is named after Karl Wilhelm Feuerbach.

In geometry, the Fermat point of a triangle, also called the Torricelli point or Fermat–Torricelli point, is a point such that the total distance from the three vertices of the triangle to the point is the minimum possible. It is so named because this problem was first raised by Fermat in a private letter to Evangelista Torricelli, who solved it.
In geometry, a triangle center is a point in the plane that is in some sense a center of a triangle akin to the centers of squares and circles, that is, a point that is in the middle of the figure by some measure. For example the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.
In geometry, Napoleon points are a pair of special points associated with a plane triangle. It is generally believed that the existence of these points was discovered by Napoleon Bonaparte, the Emperor of the French from 1804 to 1815, but many have questioned this belief. The Napoleon points are triangle centers and they are listed as the points X(17) and X(18) in Clark Kimberling's Encyclopedia of Triangle Centers.
In geometry, the Spieker center is a special point associated with a plane triangle. It is defined as the center of mass of the perimeter of the triangle. The Spieker center of a triangle ABC is the center of gravity of a homogeneous wire frame in the shape of triangle ABC. The point is named in honor of the 19th-century German geometer Theodor Spieker. The Spieker center is a triangle center and it is listed as the point X(10) in Clark Kimberling's Encyclopedia of Triangle Centers.
In triangle geometry, the Apollonius point is a special point associated with a plane triangle. The point is a triangle center and it is designated as X(181) in Clark Kimberling's Encyclopedia of Triangle Centers (ETC). The Apollonius center is also related to the Apollonius problem.
In triangle geometry, the Steiner point is a particular point associated with a plane triangle. It is a triangle center and it is designated as the center X(99) in Clark Kimberling's Encyclopedia of Triangle Centers. Jakob Steiner (1796–1863), Swiss mathematician, described this point in 1826. The point was given Steiner's name by Joseph Neuberg in 1886.
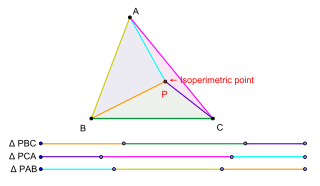
In geometry, the isoperimetric point is a special point associated with a plane triangle. The term was originally introduced by G.R. Veldkamp in a paper published in the American Mathematical Monthly in 1985 to denote a point P in the plane of a triangle ABC having the property that the triangles PBC, PCA and PAB have isoperimeters, that is, having the property that

In geometry, the Yff center of congruence is a special point associated with a triangle. This special point is a triangle center and initiated the study of this triangle center in 1987.
In geometry, the equal parallelians point is a special point associated with a plane triangle. It is a triangle center and it is denoted by X(192) in Clark Kimberling's Encyclopedia of Triangle Centers. There is a reference to this point in one of Peter Yff's notebooks, written in 1961.

In geometry the Morley centers are two special points associated with a plane triangle. Both of them are triangle centers. One of them called first Morley center is designated as X(356) in Clark Kimberling's Encyclopedia of Triangle Centers, while the other point called second Morley center is designated as X(357). The two points are also related to Morley's trisector theorem which was discovered by Frank Morley in around 1899.
In geometry the Gossard perspector is a special point associated with a plane triangle. It is a triangle center and it is designated as X(402) in Clark Kimberling's Encyclopedia of Triangle Centers. The point was named Gossard perspector by John Conway in 1998 in honour of Harry Clinton Gossard who discovered its existence in 1916. Later it was learned that the point had appeared in an article by Christopher Zeeman published during 1899 – 1902. From 2003 onwards the Encyclopedia of Triangle Centers has been referring to this point as Zeeman–Gossard perspector.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.

In Euclidean geometry, Kosnita's theorem is a property of certain circles associated with an arbitrary triangle.
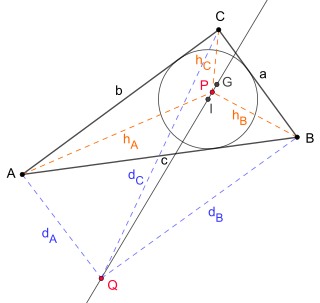
The equal detour point is a triangle center with the Kimberling number X(176). It is characterized by the equal detour property, that is if you travel from any vertex of a triangle to another by taking a detour through some inner point then the additional distance travelled is constant. This means the following equation has to hold:













