
A triangle is a polygon with three corners and three sides, one of the basic shapes in geometry. The corners, also called vertices, are zero-dimensional points while the sides connecting them, also called edges, are one-dimensional line segments. The triangle's interior is a two-dimensional region. Sometimes an arbitrary edge is chosen to be the base, in which case the opposite vertex is called the apex.

In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
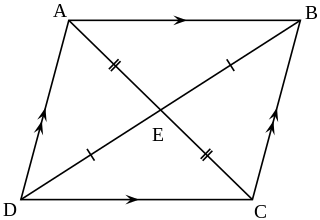
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.

In geometry, an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the side opposite the vertex. This line containing the opposite side is called the extended base of the altitude. The intersection of the extended base and the altitude is called the foot of the altitude. The length of the altitude, often simply called "the altitude", is the distance between the extended base and the vertex. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. It is a special case of orthogonal projection.

In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches the three sides. The center of the incircle is a triangle center called the triangle's incenter.

In geometry, an orthocentric system is a set of four points on a plane, one of which is the orthocenter of the triangle formed by the other three. Equivalently, the lines passing through disjoint pairs among the points are perpendicular, and the four circles passing through any three of the four points have the same radius.

In geometry, a triangle center or triangle centre is a point in the triangle's plane that is in some sense in the middle of the triangle. For example, the centroid, circumcenter, incenter and orthocenter were familiar to the ancient Greeks, and can be obtained by simple constructions.
In geometry, Napoleon points are a pair of special points associated with a plane triangle. It is generally believed that the existence of these points was discovered by Napoleon Bonaparte, the Emperor of the French from 1804 to 1815, but many have questioned this belief. The Napoleon points are triangle centers and they are listed as the points X(17) and X(18) in Clark Kimberling's Encyclopedia of Triangle Centers.
In geometry, the Spieker center is a special point associated with a plane triangle. It is defined as the center of mass of the perimeter of the triangle. The Spieker center of a triangle △ABC is the center of gravity of a homogeneous wire frame in the shape of △ABC. The point is named in honor of the 19th-century German geometer Theodor Spieker. The Spieker center is a triangle center and it is listed as the point X(10) in Clark Kimberling's Encyclopedia of Triangle Centers.
In triangle geometry, the Steiner point is a particular point associated with a triangle. It is a triangle center and it is designated as the center X(99) in Clark Kimberling's Encyclopedia of Triangle Centers. Jakob Steiner (1796–1863), Swiss mathematician, described this point in 1826. The point was given Steiner's name by Joseph Neuberg in 1886.
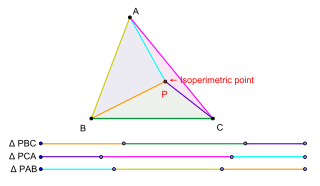
In geometry, the isoperimetric point is a triangle center — a special point associated with a plane triangle. The term was originally introduced by G.R. Veldkamp in a paper published in the American Mathematical Monthly in 1985 to denote a point P in the plane of a triangle △ABC having the property that the triangles △PBC, △PCA, △PAB have isoperimeters, that is, having the property that
In geometry, the congruent isoscelizers point is a special point associated with a plane triangle. It is a triangle center and it is listed as X(173) in Clark Kimberling's Encyclopedia of Triangle Centers. This point was introduced to the study of triangle geometry by Peter Yff in 1989.
In geometry, the equal parallelians point is a special point associated with a plane triangle. It is a triangle center and it is denoted by X(192) in Clark Kimberling's Encyclopedia of Triangle Centers. There is a reference to this point in one of Peter Yff's notebooks, written in 1961.
In geometry the Gossard perspector is a special point associated with a plane triangle. It is a triangle center and it is designated as X(402) in Clark Kimberling's Encyclopedia of Triangle Centers. The point was named Gossard perspector by John Conway in 1998 in honour of Harry Clinton Gossard who discovered its existence in 1916. Later it was learned that the point had appeared in an article by Christopher Zeeman published during 1899 – 1902. From 2003 onwards the Encyclopedia of Triangle Centers has been referring to this point as Zeeman–Gossard perspector.
In geometry, central lines are certain special straight lines that lie in the plane of a triangle. The special property that distinguishes a straight line as a central line is manifested via the equation of the line in trilinear coordinates. This special property is related to the concept of triangle center also. The concept of a central line was introduced by Clark Kimberling in a paper published in 1994.
In Euclidean geometry, a triangle conic is a conic in the plane of the reference triangle and associated with it in some way. For example, the circumcircle and the incircle of the reference triangle are triangle conics. Other examples are the Steiner ellipse, which is an ellipse passing through the vertices and having its centre at the centroid of the reference triangle; the Kiepert hyperbola which is a conic passing through the vertices, the centroid and the orthocentre of the reference triangle; and the Artzt parabolas, which are parabolas touching two sidelines of the reference triangle at vertices of the triangle.
In geometry, a central triangle is a triangle in the plane of the reference triangle. The trilinear coordinates of its vertices relative to the reference triangle are expressible in a certain cyclical way in terms of two functions having the same degree of homogeneity. At least one of the two functions must be a triangle center function. The excentral triangle is an example of a central triangle. The central triangles have been classified into three types based on the properties of the two functions.
In Euclidean geometry, a circumcevian triangle is a special triangle associated with a reference triangle and a point in the plane of the triangle. It is also associated with the circumcircle of the reference triangle.

In mathematics, modern triangle geometry, or new triangle geometry, is the body of knowledge relating to the properties of a triangle discovered and developed roughly since the beginning of the last quarter of the nineteenth century. Triangles and their properties were the subject of investigation since at least the time of Euclid. In fact, Euclid's Elements contains description of the four special points – centroid, incenter, circumcenter and orthocenter - associated with a triangle. Even though Pascal and Ceva in the seventeenth century, Euler in the eighteenth century and Feuerbach in the nineteenth century and many other mathematicians had made important discoveries regarding the properties of the triangle, it was the publication in 1873 of a paper by Emile Lemoine (1840–1912) with the title "On a remarkable point of the triangle" that was considered to have, according to Nathan Altschiller-Court, "laid the foundations...of the modern geometry of the triangle as a whole." The American Mathematical Monthly, in which much of Lemoine's work is published, declared that "To none of these [geometers] more than Émile-Michel-Hyacinthe Lemoine is due the honor of starting this movement of modern triangle geometry". The publication of this paper caused a remarkable upsurge of interest in investigating the properties of the triangle during the last quarter of the nineteenth century and the early years of the twentieth century. A hundred-page article on triangle geometry in Klein's Encyclopedia of Mathematical Sciences published in 1914 bears witness to this upsurge of interest in triangle geometry.
In triangle geometry, the Kiepert conics are two special conics associated with the reference triangle. One of them is a hyperbola, called the Kiepert hyperbola and the other is a parabola, called the Kiepert parabola. The Kiepert conics are defined as follows:
![.mw-parser-output .legend{page-break-inside:avoid;break-inside:avoid-column}.mw-parser-output .legend-color{display:inline-block;min-width:1.25em;height:1.25em;line-height:1.25;margin:1px 0;text-align:center;border:1px solid black;background-color:transparent;color:black}.mw-parser-output .legend-text{}
Reference triangle ^ABC
^A'P2Q3 [?]
^Q1B'P3 [?]
^P1Q2C' [?]
^A'B'C' (Yff central triangle) Yff center of congruence.svg](http://upload.wikimedia.org/wikipedia/commons/thumb/a/a3/Yff_center_of_congruence.svg/300px-Yff_center_of_congruence.svg.png)













