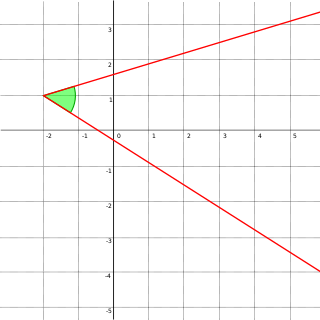
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays lie in the plane that contains the rays. Angles are also formed by the intersection of two planes. These are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.

Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the Euclidean plane. The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics.

In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle. The condition of perpendicularity may be represented graphically using the perpendicular symbol, ⟂. It can be defined between two lines, between a line and a plane, and between two planes.

Angle trisection is a classical problem of straightedge and compass construction of ancient Greek mathematics. It concerns construction of an angle equal to one third of a given arbitrary angle, using only two tools: an unmarked straightedge and a compass.

Elliptic geometry is an example of a geometry in which Euclid's parallel postulate does not hold. Instead, as in spherical geometry, there are no parallel lines since any two lines must intersect. However, unlike in spherical geometry, two lines are usually assumed to intersect at a single point. Because of this, the elliptic geometry described in this article is sometimes referred to as single elliptic geometry whereas spherical geometry is sometimes referred to as double elliptic geometry.

In mathematics, hyperbolic geometry is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:

In the branch of mathematics known as Euclidean geometry, the Poncelet–Steiner theorem is one of several results concerning compass and straightedge constructions with additional restrictions imposed. This result states that whatever can be constructed by straightedge and compass together can be constructed by straightedge alone, provided that a single circle and its centre are given. This theorem is related to the rusty compass equivalence.
In geometry, parallel lines are coplanar straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. Parallel curves are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called skew lines.

Absolute geometry is a geometry based on an axiom system for Euclidean geometry without the parallel postulate or any of its alternatives. Traditionally, this has meant using only the first four of Euclid's postulates, but since these are not sufficient as a basis of Euclidean geometry, other systems, such as Hilbert's axioms without the parallel axiom, are used. The term was introduced by János Bolyai in 1832. It is sometimes referred to as neutral geometry, as it is neutral with respect to the parallel postulate.
In geometry, hyperbolic motions are isometric automorphisms of a hyperbolic space. Under composition of mappings, the hyperbolic motions form a continuous group. This group is said to characterize the hyperbolic space. Such an approach to geometry was cultivated by Felix Klein in his Erlangen program. The idea of reducing geometry to its characteristic group was developed particularly by Mario Pieri in his reduction of the primitive notions of geometry to merely point and motion.
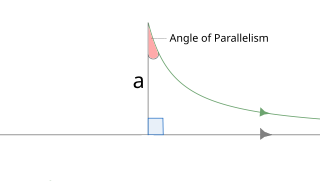
In hyperbolic geometry, the angle of parallelism , is the angle at the non-right angle vertex of a right hyperbolic triangle having two asymptotic parallel sides. The angle depends on the segment length a between the right angle and the vertex of the angle of parallelism.
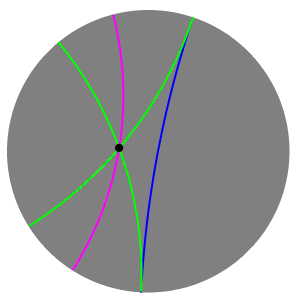
In hyperbolic geometry, two lines may intersect, be ultraparallel, or be limiting parallel.

In geometry, the Wythoff symbol is a notation representing a Wythoff construction of a uniform polyhedron or plane tiling within a Schwarz triangle. It was first used by Coxeter, Longuet-Higgins and Miller in their enumeration of the uniform polyhedra. Later the Coxeter diagram was developed to mark uniform polytopes and honeycombs in n-dimensional space within a fundamental simplex.

A Saccheri quadrilateral is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book Euclides ab omni naevo vindicatus first published in 1733, an attempt to prove the parallel postulate using the method Reductio ad absurdum. The Saccheri quadrilateral may occasionally be referred to as the Khayyam–Saccheri quadrilateral, in reference to the 11th century Persian scholar Omar Khayyam.

In hyperbolic geometry, an ideal point, omega point or point at infinity is a well-defined point outside the hyperbolic plane or space. Given a line l and a point P not on l, right- and left-limiting parallels to l through P converge to l at ideal points.

In geometry, Apollonian circles are two families (pencils) of circles such that every circle in the first family intersects every circle in the second family orthogonally, and vice versa. These circles form the basis for bipolar coordinates. They were discovered by Apollonius of Perga, a renowned Greek geometer.

In hyperbolic geometry, a hypercycle, hypercircle or equidistant curve is a curve whose points have the same orthogonal distance from a given straight line.

In hyperbolic geometry, a horocycle, sometimes called an oricycle, oricircle, or limit circle, is a curve whose normal or perpendicular geodesics all converge asymptotically in the same direction. It is the two-dimensional case of a horosphere.
Foundations of geometry is the study of geometries as axiomatic systems. There are several sets of axioms which give rise to Euclidean geometry or to non-Euclidean geometries. These are fundamental to the study and of historical importance, but there are a great many modern geometries that are not Euclidean which can be studied from this viewpoint. The term axiomatic geometry can be applied to any geometry that is developed from an axiom system, but is often used to mean Euclidean geometry studied from this point of view. The completeness and independence of general axiomatic systems are important mathematical considerations, but there are also issues to do with the teaching of geometry which come into play.
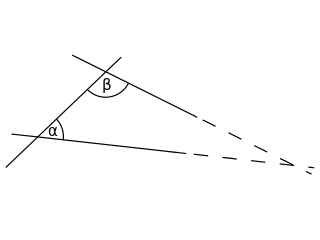
In geometry, the parallel postulate, also called Euclid's fifth postulate because it is the fifth postulate in Euclid's Elements, is a distinctive axiom in Euclidean geometry. It states that, in two-dimensional geometry:
If a line segment intersects two straight lines forming two interior angles on the same side that are less than two right angles, then the two lines, if extended indefinitely, meet on that side on which the angles sum to less than two right angles.



















