Contour set

Last updated December 10, 2021

In mathematics, contour sets generalize and formalize the everyday notions of

Formal definitions

Given a relation on pairs of elements of set $X$

\succcurlyeq ~\subseteq ~X^{2}

and an element $x$ of $X$

x\in X

The upper contour set of $x$ is the set of all $y$ that are related to $x$ :

\left\{y~\backepsilon ~y\succcurlyeq x\right\}

The lower contour set of $x$ is the set of all $y$ such that $x$ is related to them:

\left\{y~\backepsilon ~x\succcurlyeq y\right\}

The strict upper contour set of $x$ is the set of all $y$ that are related to $x$ without $x$ being in this way related to any of them:

\left\{y~\backepsilon ~(y\succcurlyeq x)\land \lnot (x\succcurlyeq y)\right\}

The strict lower contour set of $x$ is the set of all $y$ such that $x$ is related to them without any of them being in this way related to $x$ :

\left\{y~\backepsilon ~(x\succcurlyeq y)\land \lnot (y\succcurlyeq x)\right\}

The formal expressions of the last two may be simplified if we have defined

\succ ~=~\left\{\left(a,b\right)~\backepsilon ~\left(a\succcurlyeq b\right)\land \lnot (b\succcurlyeq a)\right\}

so that $a$ is related to $b$ but $b$ is not related to $a$ , in which case the strict upper contour set of $x$ is

\left\{y~\backepsilon ~y\succ x\right\}

and the strict lower contour set of $x$ is

\left\{y~\backepsilon ~x\succ y\right\}

Contour sets of a function

In the case of a function $f()$ considered in terms of relation $\triangleright$ , reference to the contour sets of the function is implicitly to the contour sets of the implied relation

(a\succcurlyeq b)~\Leftarrow ~[f(a)\triangleright f(b)]

Examples

Arithmetic

Consider a real number $x$ , and the relation $\geq$ . Then

the upper contour set of $x$ would be the set of numbers that were greater than or equal to $x$ ,
the strict upper contour set of $x$ would be the set of numbers that were greater than $x$ ,
the lower contour set of $x$ would be the set of numbers that were less than or equal to $x$ , and
the strict lower contour set of $x$ would be the set of numbers that were less than $x$ .

Consider, more generally, the relation

(a\succcurlyeq b)~\Leftarrow ~[f(a)\geq f(b)]

Then

the upper contour set of $x$ would be the set of all $y$ such that $f(y)\geq f(x)$ ,
the strict upper contour set of $x$ would be the set of all $y$ such that $f(y)>f(x)$ ,
the lower contour set of $x$ would be the set of all $y$ such that $f(x)\geq f(y)$ , and
the strict lower contour set of $x$ would be the set of all $y$ such that $f(x)>f(y)$ .

It would be technically possible to define contour sets in terms of the relation

(a\succcurlyeq b)~\Leftarrow ~[f(a)\leq f(b)]

though such definitions would tend to confound ready understanding.

In the case of a real-valued function $f()$ (whose arguments might or might not be themselves real numbers), reference to the contour sets of the function is implicitly to the contour sets of the relation

(a\succcurlyeq b)~\Leftarrow ~[f(a)\geq f(b)]

Note that the arguments to $f()$ might be vectors, and that the notation used might instead be

[(a_{1},a_{2},\ldots )\succcurlyeq (b_{1},b_{2},\ldots )]~\Leftarrow ~[f(a_{1},a_{2},\ldots )\geq f(b_{1},b_{2},\ldots )]

Economics

In economics, the set $X$ could be interpreted as a set of goods and services or of possible outcomes, the relation $\succ$ as strict preference , and the relationship $\succcurlyeq$ as weak preference. Then

the upper contour set, or better set,^[1] of $x$ would be the set of all goods, services, or outcomes that were at least as desired as $x$ ,
the strict upper contour set of $x$ would be the set of all goods, services, or outcomes that were more desired than $x$ ,
the lower contour set, or worse set,^[1] of $x$ would be the set of all goods, services, or outcomes that were no more desired than $x$ , and
the strict lower contour set of $x$ would be the set of all goods, services, or outcomes that were less desired than $x$ .

Such preferences might be captured by a utility function $u()$ , in which case

the upper contour set of $x$ would be the set of all $y$ such that $u(y)\geq u(x)$ ,
the strict upper contour set of $x$ would be the set of all $y$ such that $u(y)>u(x)$ ,
the lower contour set of $x$ would be the set of all $y$ such that $u(x)\geq u(y)$ , and
the strict lower contour set of $x$ would be the set of all $y$ such that $u(x)>u(y)$ .

Complementarity

On the assumption that $\succcurlyeq$ is a total ordering of $X$ , the complement of the upper contour set is the strict lower contour set.

X^{2}\backslash \left\{y~\backepsilon ~y\succcurlyeq x\right\}=\left\{y~\backepsilon ~x\succ y\right\}

X^{2}\backslash \left\{y~\backepsilon ~x\succ y\right\}=\left\{y~\backepsilon ~y\succcurlyeq x\right\}

and the complement of the strict upper contour set is the lower contour set.

X^{2}\backslash \left\{y~\backepsilon ~y\succ x\right\}=\left\{y~\backepsilon ~x\succcurlyeq y\right\}

X^{2}\backslash \left\{y~\backepsilon ~x\succcurlyeq y\right\}=\left\{y~\backepsilon ~y\succ x\right\}

Related Research Articles

In mathematics, a binary relation associates elements of one set, called the domain, with elements of another set, called the codomain. A binary relation over sets $X$ and $Y$ is a new set of ordered pairs $(x, y)$ consisting of elements $x$ in $X$ and $y$ in $Y$ . It is a generalization of the more widely understood idea of a mathematical function, but with fewer restrictions. It encodes the common concept of relation: an element $x$ is related to an element $y$ , if and only if the pair $(x, y)$ belongs to the set of ordered pairs that defines the binary relation. A binary relation is the most studied special case $n = 2$ of an $n$ -ary relation over sets $X 1, ..., X n$ , which is a subset of the Cartesian product

In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word partial in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable.

In mathematics, especially in order theory, a preorder or quasiorder is a binary relation that is reflexive and transitive. Preorders are more general than equivalence relations and (non-strict) partial orders, both of which are special cases of a preorder: an antisymmetric preorder is a partial order, and a symmetric preorder is an equivalence relation.

In mathematics, the infimum of a subset $of a partially ordered set is a greatest element in that is less than or equal to all elements of if such an element exists. Consequently, the term greatest lower bound is also commonly used.$

In mathematics, the limit inferior and limit superior of a sequence can be thought of as limiting bounds on the sequence. They can be thought of in a similar fashion for a function. For a set, they are the infimum and supremum of the set's limit points, respectively. In general, when there are multiple objects around which a sequence, function, or set accumulates, the inferior and superior limits extract the smallest and largest of them; the type of object and the measure of size is context-dependent, but the notion of extreme limits is invariant. Limit inferior is also called infimum limit, limit infimum, liminf, inferior limit, lower limit, or inner limit; limit superior is also known as supremum limit, limit supremum, limsup, superior limit, upper limit, or outer limit.

In mathematics, a monotonic function is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory.

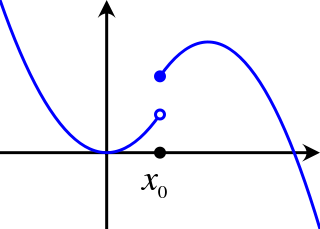
In mathematical analysis, semicontinuity is a property of extended real-valued functions that is weaker than continuity. An extended real-valued function $is upper semicontinuous at a point if, roughly speaking, the function values for arguments near are not much higher than$

In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities:

In the mathematical discipline of set theory, forcing is a technique for proving consistency and independence results. It was first used by Paul Cohen in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory.

Convex function Real function with secant line between points above the graph itself

In mathematics, a real-valued function is called convex if the line segment between any two points on the graph of the function does not lie below the graph between the two points. Equivalently, a function is convex if its epigraph is a convex set. A twice-differentiable function of a single variable is convex if and only if its second derivative is nonnegative on its entire domain. Well-known examples of convex functions of a single variable include the quadratic function $and the exponential function . In simple terms, a convex function refers to a function that is in the shape of a cup, and a concave function is in the shape of a cap .$

Symmetric difference Subset of the elements that belong to exactly one among two sets

In mathematics, the symmetric difference of two sets, also known as the disjunctive union, is the set of elements which are in either of the sets, but not in their intersection. For example, the symmetric difference of the sets $and is .$

In mathematics, a concave function is the negative of a convex function. A concave function is also synonymously called concave downwards, concave down, convex upwards, convex cap, or upper convex.

In mathematics, a Heyting algebra is a bounded lattice equipped with a binary operation a → b of implication such that ≤ b is equivalent to c ≤. From a logical standpoint, A → B is by this definition the weakest proposition for which modus ponens, the inference rule A → B, A ⊢ B, is sound. Like Boolean algebras, Heyting algebras form a variety axiomatizable with finitely many equations. Heyting algebras were introduced by Arend Heyting (1930) to formalize intuitionistic logic.

In mathematics, a level set of a real-valued function f of n real variables is a set where the function takes on a given constant value c, that is:

Categorial grammar is a family of formalisms in natural language syntax which share the central assumption that syntactic constituents combine as functions and arguments. Categorial grammar posits a close relationship between the syntax and semantic composition, since it typically treats syntactic categories as corresponding to semantic types. Categorial grammars were developed in the 1930s by Kazimierz Ajdukiewicz, Yehoshua Bar-Hillel, and Joachim Lambek. It saw a surge of interest in the 1970s following the work of Richard Montague, whose Montague grammar assumed a similar view of syntax. It continues to be a major paradigm, particularly within formal semantics.

Utility maximization was first developed by utilitarian philosophers Jeremy Bentham and John Stewart Mill. In microeconomics, the utility maximization problem is the problem consumers face: "How should I spend my money in order to maximize my utility?" It is a type of optimal decision problem. It consists of choosing how much of each available good or service to consume, taking into account a constraint on total spending (income), the prices of the goods and their preferences.

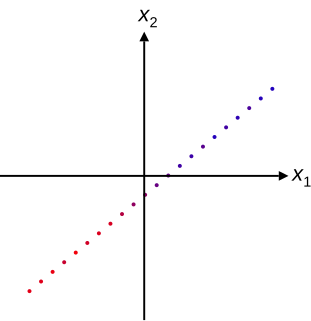
In mathematics, majorization is a preorder on vectors of real numbers. For a vector $, we denote by the vector with the same components, but sorted in descending order. Given, we say that weakly majorizes from below written as iff$

In economics, convex preferences are an individual's ordering of various outcomes, typically with regard to the amounts of various goods consumed, with the property that, roughly speaking, "averages are better than the extremes". The concept roughly corresponds to the concept of diminishing marginal utility without requiring utility functions.

The dominance-based rough set approach (DRSA) is an extension of rough set theory for multi-criteria decision analysis (MCDA), introduced by Greco, Matarazzo and Słowiński. The main change compared to the classical rough sets is the substitution for the indiscernibility relation by a dominance relation, which permits one to deal with inconsistencies typical to consideration of criteria and preference-ordered decision classes.

Single-peaked preferences are a class of preference relations. A group of agents is said to have single-peaked preferences over a set of possible outcomes if the outcomes can be ordered along a line such that:

Each agent has a "best outcome" in the set, and -
For each agent, outcomes that are further from his or her best outcome are preferred less.

References

1 2 Robert P. Gilles (1996). Economic Exchange and Social Organization: The Edgeworthian Foundations of General Equilibrium Theory. Springer. p. 35. ISBN 9780792342007.

Bibliography

Andreu Mas-Colell, Michael D. Whinston, and Jerry R. Green, Microeconomic Theory (LCC HB172.M6247 1995), p43. ISBN 0-19-507340-1 (cloth) ISBN 0-19-510268-1 (paper)

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[:0-1] 1 2 Robert P. Gilles (1996). Economic Exchange and Social Organization: The Edgeworthian Foundations of General Equilibrium Theory. Springer. p. 35. ISBN 9780792342007.

[1]