In mathematics, specifically category theory, a functor is a map between categories. Functors were first considered in algebraic topology, where algebraic objects are associated to topological spaces, and maps between these algebraic objects are associated to continuous maps between spaces. Nowadays, functors are used throughout modern mathematics to relate various categories. Thus, functors are important in all areas within mathematics to which category theory is applied.

In mathematics, a tensor is an algebraic object that describes a linear mapping from one set of algebraic objects to another. Objects that tensors may map between include, but are not limited to, vectors and scalars, and, recursively, even other tensors. Tensors are inherently related to vector spaces and their dual spaces, and can take several different forms – for example: a scalar, a vector, a dual vector at a point, or a multi-linear map between vector spaces. Euclidean vectors and scalars are the simplest tensors. While tensors are defined independent of any basis, the literature on physics often refers to them by their components in a basis related to a particular coordinate system.
Charge, parity, and time reversal symmetry is a fundamental symmetry of physical laws under the simultaneous transformations of charge conjugation (C), parity transformation (P), and time reversal (T). CPT is the only combination of C, P, and T that is observed to be an exact symmetry of nature at the fundamental level. The CPT theorem says that CPT symmetry holds for all physical phenomena, or more precisely, that any Lorentz invariant local quantum field theory with a Hermitian Hamiltonian must have CPT symmetry.
In mathematics, especially in applications of linear algebra to physics, the Einstein notation or Einstein summation convention is a notational convention that implies summation over a set of indexed terms in a formula, thus achieving notational brevity. As part of mathematics it is a notational subset of Ricci calculus; however, it is often used in applications in physics that do not distinguish between tangent and cotangent spaces. It was introduced to physics by Albert Einstein in 1916.

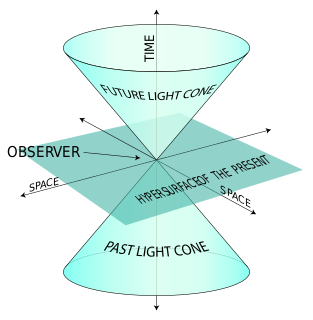
In mathematical physics, Minkowski space is a combination of three-dimensional Euclidean space and time into a four-dimensional manifold where the spacetime interval between any two events is independent of the inertial frame of reference in which they are recorded. Although initially developed by mathematician Hermann Minkowski for Maxwell's equations of electromagnetism, the mathematical structure of Minkowski spacetime was shown to be an immediate consequence of the postulates of special relativity.
In relativistic physics, Lorentz symmetry, named after Hendrik Lorentz, is an equivalence of observation or observational symmetry due to special relativity implying that the laws of physics stay the same for all observers that are moving with respect to one another within an inertial frame. It has also been described as "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space".
In theoretical physics, general covariance, also known as diffeomorphism covariance or general invariance, consists of the invariance of the form of physical laws under arbitrary differentiable coordinate transformations. The essential idea is that coordinates do not exist a priori in nature, but are only artifices used in describing nature, and hence should play no role in the formulation of fundamental physical laws.

In mathematics, an invariant is a property, held by a class of mathematical objects, which remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used. For example, the area of a triangle is an invariant with respect to isometries of the Euclidean plane. The phrases "invariant under" and "invariant to" a transformation are both used. More generally, an invariant with respect to an equivalence relation is a property that is constant on each equivalence class.
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.

The mathematics of general relativity refers to various mathematical structures and techniques that are used in studying and formulating Albert Einstein's theory of general relativity. The main tools used in this geometrical theory of gravitation are tensor fields defined on a Lorentzian manifold representing spacetime. This article is a general description of the mathematics of general relativity.
In general relativity, the hole argument is an apparent paradox that much troubled Albert Einstein while developing his famous field equations.

In physics, a symmetry of a physical system is a physical or mathematical feature of the system that is preserved or remains unchanged under some transformation.
In physics, the principle of covariance emphasizes formulation of physical laws using only those physical quantities the measurements of which the observers in different frames of reference could unambiguously correlate.
In physics, event symmetry includes invariance principles that have been used in some discrete approaches to quantum gravity where the diffeomorphism invariance of general relativity can be extended to a covariance under every permutation of spacetime events.
The light-front quantization of quantum field theories provides a useful alternative to ordinary equal-time quantization. In particular, it can lead to a relativistic description of bound systems in terms of quantum-mechanical wave functions. The quantization is based on the choice of light-front coordinates, where plays the role of time and the corresponding spatial coordinate is . Here, is the ordinary time, is one Cartesian coordinate, and is the speed of light. The other two Cartesian coordinates, and , are untouched and often called transverse or perpendicular, denoted by symbols of the type . The choice of the frame of reference where the time and -axis are defined can be left unspecified in an exactly soluble relativistic theory, but in practical calculations some choices may be more suitable than others.

In physics, a covariance group is a group of coordinate transformations between frames of reference. A frame of reference provides a set of coordinates for an observer moving with that frame to make measurements and define physical quantities. The covariance principle states the laws of physics should transform from one frame to another covariantly, that is, according to a representation of the covariance group.

In physics, a gauge theory is a type of field theory in which the Lagrangian is invariant under certain Lie groups of local transformations.












