
In geometry, an n-gonal antiprism or n-antiprism is a polyhedron composed of two parallel direct copies of an n-sided polygon, connected by an alternating band of 2ntriangles.

A quadrilateral is a polygon in Euclidean plane geometry with four edges (sides) and four vertices (corners). Other names for quadrilateral include quadrangle and tetragon. A quadrilateral with vertices , , and is sometimes denoted as .

In Euclidean plane geometry, a rectangle is a quadrilateral with four right angles. It can also be defined as: an equiangular quadrilateral, since equiangular means that all of its angles are equal ; or a parallelogram containing a right angle. A rectangle with four sides of equal length is a square. The term oblong is occasionally used to refer to a non-square rectangle. A rectangle with vertices ABCD would be denoted as ABCD.
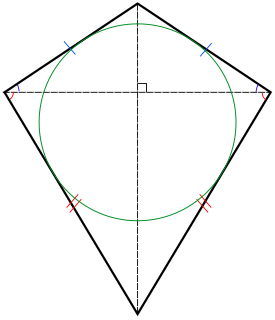
In Euclidean geometry, a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are adjacent to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite to each other instead of being adjacent. Kite quadrilaterals are named for the wind-blown, flying kites, which often have this shape and which are in turn named for a bird. Kites are also known as deltoids, but the word "deltoid" may also refer to a deltoid curve, an unrelated geometric object.
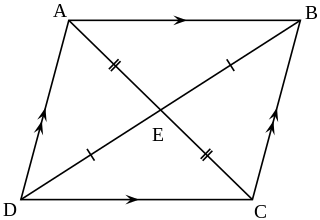
In Euclidean geometry, a parallelogram is a simple (non-self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure. The congruence of opposite sides and opposite angles is a direct consequence of the Euclidean parallel postulate and neither condition can be proven without appealing to the Euclidean parallel postulate or one of its equivalent formulations.

In plane Euclidean geometry, a rhombus is a quadrilateral whose four sides all have the same length. Another name is equilateral quadrilateral, since equilateral means that all of its sides are equal in length. The rhombus is often called a diamond, after the diamonds suit in playing cards which resembles the projection of an octahedral diamond, or a lozenge, though the former sometimes refers specifically to a rhombus with a 60° angle, and the latter sometimes refers specifically to a rhombus with a 45° angle.

In Euclidean geometry, a convex quadrilateral with at least one pair of parallel sides is referred to as a trapezium in English outside North America, but as a trapezoid in American and Canadian English. The parallel sides are called the bases of the trapezoid and the other two sides are called the legs or the lateral sides. A scalene trapezoid is a trapezoid with no sides of equal measure, in contrast with the special cases below.

In geometry, a prism is a polyhedron comprising an n-sided polygon base, a second base which is a translated copy of the first, and n other faces, necessarily all parallelograms, joining corresponding sides of the two bases. All cross-sections parallel to the bases are translations of the bases. Prisms are named after their bases; example: a prism with a pentagonal base is called a pentagonal prism. Prisms are a subclass of prismatoids.
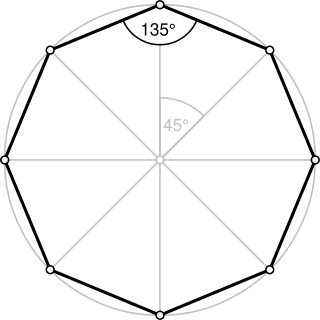
In geometry, an octagon is an eight-sided polygon or 8-gon.
In Euclidean geometry, a regular polygon is a polygon that is equiangular and equilateral. Regular polygons may be either convex or star. In the limit, a sequence of regular polygons with an increasing number of sides approximates a circle, if the perimeter or area is fixed, or a regular apeirogon, if the edge length is fixed.

In Euclidean geometry, an isosceles trapezoid is a convex quadrilateral with a line of symmetry bisecting one pair of opposite sides. It is a special case of a trapezoid. Alternatively, it can be defined as a trapezoid in which both legs and both base angles are of the same measure. Note that a non-rectangular parallelogram is not an isosceles trapezoid because of the second condition, or because it has no line of symmetry. In any isosceles trapezoid, two opposite sides are parallel, and the two other sides are of equal length. The diagonals are also of equal length. The base angles of an isosceles trapezoid are equal in measure.

In geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles. It can also be defined as a rectangle in which two adjacent sides have equal length. A square with vertices ABCD would be denoted ABCD.
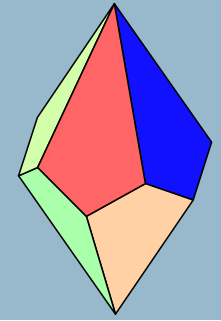
An n-gonal trapezohedron, antidipyramid, antibipyramid, or deltohedron is the dual polyhedron of an n-gonal antiprism. The 2n faces of an n-trapezohedron are congruent and symmetrically staggered; they are called twisted kites. With a higher symmetry, its 2n faces are kites.

In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex. The term originates from Kepler's names for the Archimedean solids.

In geometry, an antiparallelogram is a type of self-crossing quadrilateral. Like a parallelogram, an antiparallelogram has two opposite pairs of equal-length sides, but the sides in the longer pair cross each other as in a scissors mechanism. Antiparallelograms are also called contraparallelograms or crossed parallelograms.

In geometry, a skew polygon is a polygon whose vertices are not all coplanar. Skew polygons must have at least four vertices. The interior surface of such a polygon is not uniquely defined.
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-transitive.

In geometry, the rhombicosacron is a nonconvex isohedral polyhedron. It is the dual of the uniform rhombicosahedron, U56. It has 50 vertices, 120 edges, and 60 crossed-quadrilateral faces.
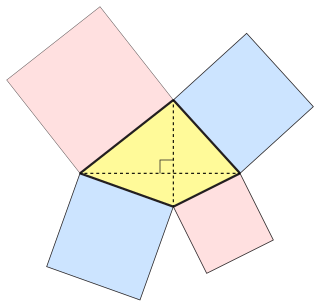
In Euclidean geometry, an orthodiagonal quadrilateral is a quadrilateral in which the diagonals cross at right angles. In other words, it is a four-sided figure in which the line segments between non-adjacent vertices are orthogonal (perpendicular) to each other.

























