General expressions
General expressions for the enthalpy H, entropy S and Gibbs free energy G are given by [1]
In thermodynamics, a departure function is defined for any thermodynamic property as the difference between the property as computed for an ideal gas and the property of the species as it exists in the real world, for a specified temperature T and pressure P. Common departure functions include those for enthalpy, entropy, and internal energy.
Departure functions are used to calculate real fluid extensive properties (i.e. properties which are computed as a difference between two states). A departure function gives the difference between the real state, at a finite volume or non-zero pressure and temperature, and the ideal state, usually at zero pressure or infinite volume and temperature.
For example, to evaluate enthalpy change between two points h(v1,T1) and h(v2,T2) we first compute the enthalpy departure function between volume v1 and infinite volume at T = T1, then add to that the ideal gas enthalpy change due to the temperature change from T1 to T2, then subtract the departure function value between v2 and infinite volume.
Departure functions are computed by integrating a function which depends on an equation of state and its derivative.
General expressions for the enthalpy H, entropy S and Gibbs free energy G are given by [1]
The Peng–Robinson equation of state relates the three interdependent state properties pressure P, temperature T, and molar volume Vm. From the state properties (P, Vm, T), one may compute the departure function for enthalpy per mole (denoted h) and entropy per mole (s): [2]
where is defined in the Peng-Robinson equation of state, Tr is the reduced temperature, Pr is the reduced pressure, Z is the compressibility factor, and
Typically, one knows two of the three state properties (P, Vm, T), and must compute the third directly from the equation of state under consideration. To calculate the third state property, it is necessary to know three constants for the species at hand: the critical temperature Tc, critical pressure Pc, and the acentric factor ω. But once these constants are known, it is possible to evaluate all of the above expressions and hence determine the enthalpy and entropy departures.

An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions.
In electrochemistry, the Nernst equation is a chemical thermodynamical relationship that permits the calculation of the reduction potential of a reaction from the standard electrode potential, absolute temperature, the number of electrons involved in the redox reaction, and activities of the chemical species undergoing reduction and oxidation respectively. It was named after Walther Nernst, a German physical chemist who formulated the equation.

In thermodynamics, the Gibbs free energy is a thermodynamic potential that can be used to calculate the maximum amount of work that may be performed by a thermodynamically closed system at constant temperature and pressure. It also provides a necessary condition for processes such as chemical reactions that may occur under these conditions.
In physics, a partition function describes the statistical properties of a system in thermodynamic equilibrium. Partition functions are functions of the thermodynamic state variables, such as the temperature and volume. Most of the aggregate thermodynamic variables of the system, such as the total energy, free energy, entropy, and pressure, can be expressed in terms of the partition function or its derivatives. The partition function is dimensionless.
In chemistry, an ideal solution or ideal mixture is a solution that exhibits thermodynamic properties analogous to those of a mixture of ideal gases. The enthalpy of mixing is zero as is the volume change on mixing by definition; the closer to zero the enthalpy of mixing is, the more "ideal" the behavior of the solution becomes. The vapor pressures of the solvent and solute obey Raoult's law and Henry's law, respectively, and the activity coefficient is equal to one for each component.
In chemical thermodynamics, the fugacity of a real gas is an effective partial pressure which replaces the mechanical partial pressure in an accurate computation of the chemical equilibrium constant. It is equal to the pressure of an ideal gas which has the same temperature and molar Gibbs free energy as the real gas.
In chemical kinetics a reaction rate constant or reaction rate coefficient, k, quantifies the rate and direction of a chemical reaction.
The Clausius–Clapeyron relation, named after Rudolf Clausius and Benoît Paul Émile Clapeyron, specifies the temperature dependence of pressure, most importantly vapor pressure, at a discontinuous phase transition between two phases of matter of a single constituent. Its relevance to meteorology and climatology is the increase of the water-holding capacity of the atmosphere by about 7% for every 1 °C (1.8 °F) rise in temperature.

In probability theory and directional statistics, the von Mises distribution is a continuous probability distribution on the circle. It is a close approximation to the wrapped normal distribution, which is the circular analogue of the normal distribution. A freely diffusing angle on a circle is a wrapped normally distributed random variable with an unwrapped variance that grows linearly in time. On the other hand, the von Mises distribution is the stationary distribution of a drift and diffusion process on the circle in a harmonic potential, i.e. with a preferred orientation. The von Mises distribution is the maximum entropy distribution for circular data when the real and imaginary parts of the first circular moment are specified. The von Mises distribution is a special case of the von Mises–Fisher distribution on the N-dimensional sphere.
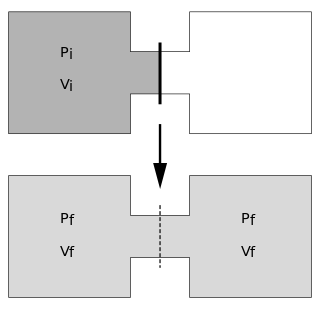
The Joule expansion is an irreversible process in thermodynamics in which a volume of gas is kept in one side of a thermally isolated container, with the other side of the container being evacuated. The partition between the two parts of the container is then opened, and the gas fills the whole container.

The chemists Peter Debye and Erich Hückel noticed that solutions that contain ionic solutes do not behave ideally even at very low concentrations. So, while the concentration of the solutes is fundamental to the calculation of the dynamics of a solution, they theorized that an extra factor that they termed gamma is necessary to the calculation of the activity coefficients of the solution. Hence they developed the Debye–Hückel equation and Debye–Hückel limiting law. The activity is only proportional to the concentration and is altered by a factor known as the activity coefficient . This factor takes into account the interaction energy of ions in solution.

The thermodynamic properties of materials are intensive thermodynamic parameters which are specific to a given material. Each is directly related to a second order differential of a thermodynamic potential. Examples for a simple 1-component system are:
The Eyring equation is an equation used in chemical kinetics to describe changes in the rate of a chemical reaction against temperature. It was developed almost simultaneously in 1935 by Henry Eyring, Meredith Gwynne Evans and Michael Polanyi. The equation follows from the transition state theory, also known as activated-complex theory. If one assumes a constant enthalpy of activation and constant entropy of activation, the Eyring equation is similar to the empirical Arrhenius equation, despite the Arrhenius equation being empirical and the Eyring equation based on statistical mechanical justification.
The Van 't Hoff equation relates the change in the equilibrium constant, Keq, of a chemical reaction to the change in temperature, T, given the standard enthalpy change, ΔrH⊖, for the process. It was proposed by Dutch chemist Jacobus Henricus van 't Hoff in 1884 in his book Études de Dynamique chimique.

Thermodynamic databases contain information about thermodynamic properties for substances, the most important being enthalpy, entropy, and Gibbs free energy. Numerical values of these thermodynamic properties are collected as tables or are calculated from thermodynamic datafiles. Data is expressed as temperature-dependent values for one mole of substance at the standard pressure of 101.325 kPa, or 100 kPa. Unfortunately, both of these definitions for the standard condition for pressure are in use.

In chemistry, transition state theory (TST) explains the reaction rates of elementary chemical reactions. The theory assumes a special type of chemical equilibrium (quasi-equilibrium) between reactants and activated transition state complexes.
In chemical thermodynamics, excess properties are properties of mixtures which quantify the non-ideal behavior of real mixtures. They are defined as the difference between the value of the property in a real mixture and the value that would exist in an ideal solution under the same conditions. The most frequently used excess properties are the excess volume, excess enthalpy, and excess chemical potential. The excess volume, internal energy, and enthalpy are identical to the corresponding mixing properties; that is,

Entropy production is the amount of entropy which is produced in any irreversible processes such as heat and mass transfer processes including motion of bodies, heat exchange, fluid flow, substances expanding or mixing, anelastic deformation of solids, and any irreversible thermodynamic cycle, including thermal machines such as power plants, heat engines, refrigerators, heat pumps, and air conditioners.
Heat transfer physics describes the kinetics of energy storage, transport, and energy transformation by principal energy carriers: phonons, electrons, fluid particles, and photons. Heat is energy stored in temperature-dependent motion of particles including electrons, atomic nuclei, individual atoms, and molecules. Heat is transferred to and from matter by the principal energy carriers. The state of energy stored within matter, or transported by the carriers, is described by a combination of classical and quantum statistical mechanics. The energy is different made (converted) among various carriers. The heat transfer processes are governed by the rates at which various related physical phenomena occur, such as the rate of particle collisions in classical mechanics. These various states and kinetics determine the heat transfer, i.e., the net rate of energy storage or transport. Governing these process from the atomic level to macroscale are the laws of thermodynamics, including conservation of energy.
Kaniadakis statistics is a generalization of the ordinary Boltzmann-Gibbs statistical mechanics, based on a new entropic functional commonly referred to as Kaniadakis entropy or κ-entropy, introduced as the relativistic generalization of the classical Boltzmann-Gibbs-Shannon entropy, by the Greek-Italian physicist Giorgio Kaniadakis in 2001. The κ-statistical mechanics preserves the main features of ordinary statistical mechanics and has attracted the interest of many researchers in the last decades. The κ-distribution is currently considered one of the most viable candidates for explaining complex physical, natural or artificial systems involving power-law tailed statistical distributions. The κ-statistics has been adopted successfully in the description of a variety of systems in the fields of cosmology and astrophysics, condensed matter, quantum physics, seismology, genomics, economy, epidemiology, among many others.