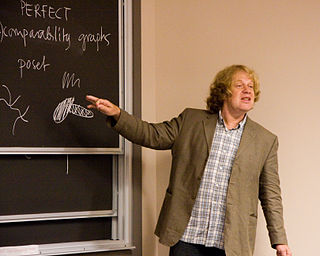Ronald Lewis Graham was an American mathematician credited by the American Mathematical Society as "one of the principal architects of the rapid development worldwide of discrete mathematics in recent years". He was president of both the American Mathematical Society and the Mathematical Association of America, and his honors included the Leroy P. Steele Prize for lifetime achievement and election to the National Academy of Sciences.
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.
The Kepler conjecture, named after the 17th-century mathematician and astronomer Johannes Kepler, is a mathematical theorem about sphere packing in three-dimensional Euclidean space. It states that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic close packing and hexagonal close packing arrangements. The density of these arrangements is around 74.05%.

In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing problems can be generalised to consider unequal spheres, spaces of other dimensions or to non-Euclidean spaces such as hyperbolic space.
The Fulkerson Prize for outstanding papers in the area of discrete mathematics is sponsored jointly by the Mathematical Optimization Society (MOS) and the American Mathematical Society (AMS). Up to three awards of $1,500 each are presented at each (triennial) International Symposium of the MOS. Originally, the prizes were paid out of a memorial fund administered by the AMS that was established by friends of the late Delbert Ray Fulkerson to encourage mathematical excellence in the fields of research exemplified by his work. The prizes are now funded by an endowment administered by MPS.

Branko Grünbaum was a Croatian-born mathematician of Jewish descent and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel.

Thomas Callister Hales is an American mathematician working in the areas of representation theory, discrete geometry, and formal verification. In representation theory he is known for his work on the Langlands program and the proof of the fundamental lemma over the group Sp(4). In discrete geometry, he settled the Kepler conjecture on the density of sphere packings and the honeycomb conjecture. In 2014, he announced the completion of the Flyspeck Project, which formally verified the correctness of his proof of the Kepler conjecture.
László Fejes Tóth was a Hungarian mathematician who specialized in geometry. He proved that a lattice pattern is the most efficient way to pack centrally symmetric convex sets on the Euclidean plane. He also investigated the sphere packing problem. He was the first to show, in 1953, that proof of the Kepler conjecture can be reduced to a finite case analysis and, later, that the problem might be solved using a computer.
The Borsuk problem in geometry, for historical reasons incorrectly called Borsuk's conjecture, is a question in discrete geometry. It is named after Karol Borsuk.

In geometry, circle packing is the study of the arrangement of circles on a given surface such that no overlapping occurs and so that no circle can be enlarged without creating an overlap. The associated packing density, η, of an arrangement is the proportion of the surface covered by the circles. Generalisations can be made to higher dimensions – this is called sphere packing, which usually deals only with identical spheres.

In geometry, tetrahedron packing is the problem of arranging identical regular tetrahedra throughout three-dimensional space so as to fill the maximum possible fraction of space.
Polyhedral combinatorics is a branch of mathematics, within combinatorics and discrete geometry, that studies the problems of counting and describing the faces of convex polyhedra and higher-dimensional convex polytopes.

Gil Kalai is an Israeli mathematician and computer scientist. He is the Henry and Manya Noskwith Professor Emeritus of Mathematics at the Hebrew University of Jerusalem, Israel, Professor of Computer Science at the Interdisciplinary Center, Herzliya, and adjunct Professor of mathematics and of computer science at Yale University, United States.
In polyhedral combinatorics, a branch of mathematics, Steinitz's theorem is a characterization of the undirected graphs formed by the edges and vertices of three-dimensional convex polyhedra: they are exactly the 3-vertex-connected planar graphs. That is, every convex polyhedron forms a 3-connected planar graph, and every 3-connected planar graph can be represented as the graph of a convex polyhedron. For this reason, the 3-connected planar graphs are also known as polyhedral graphs.
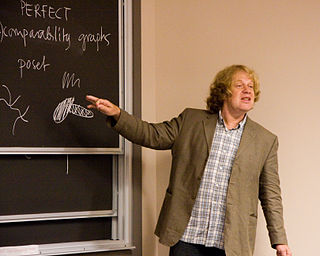
János Pach is a mathematician and computer scientist working in the fields of combinatorics and discrete and computational geometry.

Károly Bezdek is a Hungarian-Canadian mathematician. He is a professor as well as a Canada Research Chair of mathematics and the director of the Centre for Computational and Discrete Geometry at the University of Calgary in Calgary, Alberta, Canada. Also he is a professor of mathematics at the University of Pannonia in Veszprém, Hungary. His main research interests are in geometry in particular, in combinatorial, computational, convex, and discrete geometry. He has authored 3 books and more than 130 research papers. He is a founding Editor-in-Chief of the e-journal Contributions to Discrete Mathematics (CDM).
In discrete geometry, the Erdős distinct distances problem states that every set of points in the plane has a nearly-linear number of distinct distances. It was posed by Paul Erdős in 1946 and almost proven by Larry Guth and Nets Katz in 2015.

Francisco (Paco) Santos Leal is a Spanish mathematician at the University of Cantabria, known for finding a counterexample to the Hirsch conjecture in polyhedral combinatorics. In 2015 he won the Fulkerson Prize for this research.

Karim Alexander Adiprasito is a German mathematician working at the University of Copenhagen and the Hebrew University of Jerusalem who works in combinatorics. He completed his PhD in 2013 at Free University Berlin under the supervision of Günter M. Ziegler. He has been a professor at the Hebrew University since 2015, and at the University of Copenhagen since 2019. He is of German and Indonesian descent, and bears an Indonesian surname.