Combinatorial computational geometry
General-purpose textbooks
- Franco P. Preparata; Michael Ian Shamos (1985). Computational Geometry - An Introduction . Springer-Verlag. ISBN 0-387-96131-3. 1st edition; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3; Russian translation, 1989: ISBN 5-03-001041-6.
- The book is the first comprehensive monograph on the level of a graduate textbook to systematically cover the fundamental aspects of the emerging discipline of computational geometry. It is written by founders of the field and the first edition covered all major developments in the preceding 10 years.
- In the aspect of comprehensiveness it was preceded only by the 1984 survey paper, Lee, D, T., Preparata, F. P.: "Computational geometry - a survey". IEEE Trans. on Computers . Vol. 33, No. 12, pp. 1072–1101 (1984). It is focused on two-dimensional problems, but also has digressions into higher dimensions. [1] [2]
- The initial core of the book was M.I.Shamos' doctoral dissertation, which was suggested to turn into a book by a yet another pioneer in the field, Ronald Graham.
- The introduction covers the history of the field, basic data structures, and necessary notions from the theory of computation and geometry.
- The subsequent sections cover geometric searching (point location, range searching), convex hull computation, proximity-related problems (closest points, computation and applications of the Voronoi diagram, Euclidean minimum spanning tree, triangulations, etc.), geometric intersection problems, algorithms for sets of isothetic rectangles
- Herbert Edelsbrunner (1987). Algorithms in Combinatorial Geometry . Springer-Verlag. ISBN 0-89791-517-8.
- The monograph is a rather advanced exposition of problems and approaches in computational geometry focused on the role of hyperplane arrangements, which are shown to constitute a basic underlying combinatorial-geometric structure in certain areas of the field. The primary target audience are active theoretical researchers in the field, rather than application developers. Unlike most of books in computational geometry focused on 2- and 3-dimensional problems (where most applications of computational geometry are), the book aims to treat its subject in the general multi-dimensional setting. [3]
- Mark de Berg; Otfried Cheong; Marc van Kreveld; Mark Overmars (2008). Computational Geometry (3rd revised ed.). Springer-Verlag. ISBN 978-3-540-77973-5. 1st edition (1997): ISBN 3-540-61270-X.
- The textbook provides an introduction to computation geometry from the point of view of practical applications. Starting with an introduction chapter, each of the 15 remaining ones formulates a real application problem, formulates an underlying geometrical problem, and discusses techniques of computational geometry useful for its solution, with algorithms provided in pseudocode. The book treats mostly 2- and 3-dimensional geometry.
- The goal of the book is to provide a comprehensive introduction into methods and approached, rather than the cutting edge of the research in the field: the presented algorithms provide transparent and reasonably efficient solutions based on fundamental "building blocks" of computational geometry. [4] [5]
- The book consists of the following chapters (which provide both solutions for the topic of the title and its applications): "Computational Geometry (Introduction)" "Line Segment Intersection", "Polygon Triangulation", "Linear Programming", "Orthogonal Range Searching", "Point Location", "Voronoi Diagrams", "Arrangements and Duality", "Delaunay Triangulations", "More Geometric Data Structures", "Convex Hulls", "Binary Space Partitions", "Robot Motion Planning", "Quadtrees", "Visibility Graphs", "Simplex Range Searching".
- Jean-Daniel Boissonnat; Mariette Yvinec (1998). Algorithmic Geometry. Cambridge University Press. ISBN 0-521-56529-4. Translation of a 1995 French edition.
- Joseph O'Rourke (1998). Computational Geometry in C (2nd ed.). Cambridge University Press. ISBN 0-521-64976-5.
- Satyan Devadoss; Joseph O'Rourke (2011). Discrete and Computational Geometry. Princeton University Press. ISBN 978-0-691-14553-2.
- Jim Arlow (2014). Interactive Computational Geometry - A taxonomic approach. Mountain Way Limited. ISBN 978-0-9572928-2-6. 1st edition.
- This book is an interactive introduction to the fundamental algorithms of computational geometry, formatted as an interactive document viewable using software based on Mathematica.
Specialized textbooks and monographs
- Selim G. Akl; Kelly A. Lyons (1993). Parallel Computational Geometry. Prentice-Hall. ISBN 0-13-652017-0.
- Franz Aurenhammer; Rolf Klein; Der-Tsai Lee (2013). Voronoi Diagrams and Delaunay Triangulations. World Scientific.
- Erik D. Demaine; Joseph O'Rourke (2007). Geometric Folding Algorithms: Linkages, Origami, Polyhedra. Cambridge University Press. ISBN 978-0-521-85757-4.
- Efi Fogel; Dan Halperin; Ron Wein (2012). CGAL Arrangements and Their Applications, A Step-by-Step Guide. Springer-Verlag. ISBN 978-3-642-17283-0.
- Clara I. Grima & Alberto Márquez (1990). Computational Geometry on Surfaces: Performing Computational Geometry on the Cylinder, the Sphere, the Torus, and the Cone. Kluwer Academic Publishers. ISBN 1-4020-0202-5.
- Fajie Li; Reinhard Klette (2011). Euclidean Shortest Paths. Springer-Verlag. ISBN 978-1-4471-2255-5.
- Kurt Mehlhorn (1984). Data Structures and Efficient Algorithms 3: Multi-dimensional Searching and Computational Geometry. Springer-Verlag.
- Kurt Mehlhorn; Stefan Näher (1999). LEDA, A Platform for Combinatorial and Geometric Computing. Cambridge University Press. ISBN 0-521-56329-1.
- Ketan Mulmuley (1994). Computational Geometry: An Introduction Through Randomized Algorithms. Prentice-Hall. ISBN 0-13-336363-5.
- Giri Narasimhan; Michiel Smid (2007). Geometric Spanner Networks. Cambridge University Press. ISBN 978-0-521-81513-0.
- Atsuyuki Okabe; Barry Boots; Kokichi Sugihara; Sung Nok Chiu (2000). Spatial Tessellations: Concepts and Applications of Voronoi Diagrams (2nd ed.). John Wiley & Sons.
- Joseph O'Rourke (1987). Art Gallery Theorems and Algorithms. Oxford University Press.
- János Pach; Pankaj K. Agarwal (1995). Combinatorial Geometry . John Wiley and Sons. ISBN 0-471-58890-3.
- Hanan Samet (1990). The Design and Analysis of Spatial Data Structures . Addison-Wesley. ISBN 978-0-201-50255-8.
- Philip J. Schneider; David H. Eberly (2002). Geometric Tools for Computer Graphics. Morgan Kaufmann.
- Micha Sharir; Pankaj K. Agarwal (1995). Davenport–Schinzel Sequences and Their Geometric Applications. Cambridge University Press. ISBN 0-521-47025-0.
- Ghosh, Subir Kumar (2007). Visibility Algorithms in the Plane. Cambridge University Press. ISBN 978-0-521-87574-5.
- Boissonnat, Jean-Daniel; Chazal, Frédéric; Yvinec, Mariette (2018). Geometric and Topological Inference. Cambridge Texts in Applied Mathematics. Cambridge University Press.
Related Research Articles

Algebraic geometry is a branch of mathematics which uses abstract algebraic techniques, mainly from commutative algebra, to solve geometrical problems. Classically, it studies zeros of multivariate polynomials; the modern approach generalizes this in a few different aspects.

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".

In computational geometry, a Delaunay triangulation or Delone triangulation of a set of points in the plane subdivides their convex hull into triangles whose circumcircles do not contain any of the points. This maximizes the size of the smallest angle in any of the triangles, and tends to avoid sliver triangles.
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational geometry. While modern computational geometry is a recent development, it is one of the oldest fields of computing with a history stretching back to antiquity.

In mathematics, a Voronoi diagram is a partition of a plane into regions close to each of a given set of objects. It can be classified also as a tessellation. In the simplest case, these objects are just finitely many points in the plane. For each seed there is a corresponding region, called a Voronoi cell, consisting of all points of the plane closer to that seed than to any other. The Voronoi diagram of a set of points is dual to that set's Delaunay triangulation.

Geometry of numbers is the part of number theory which uses geometry for the study of algebraic numbers. Typically, a ring of algebraic integers is viewed as a lattice in and the study of these lattices provides fundamental information on algebraic numbers. The geometry of numbers was initiated by Hermann Minkowski.

Discrete geometry and combinatorial geometry are branches of geometry that study combinatorial properties and constructive methods of discrete geometric objects. Most questions in discrete geometry involve finite or discrete sets of basic geometric objects, such as points, lines, planes, circles, spheres, polygons, and so forth. The subject focuses on the combinatorial properties of these objects, such as how they intersect one another, or how they may be arranged to cover a larger object.

A triangulation of a set of points in the Euclidean space is a simplicial complex that covers the convex hull of , and whose vertices belong to . In the plane, triangulations are made up of triangles, together with their edges and vertices. Some authors require that all the points of are vertices of its triangulations. In this case, a triangulation of a set of points in the plane can alternatively be defined as a maximal set of non-crossing edges between points of . In the plane, triangulations are special cases of planar straight-line graphs.
The art gallery problem or museum problem is a well-studied visibility problem in computational geometry. It originates from the following real-world problem:
"In an art gallery, what is the minimum number of guards who together can observe the whole gallery?"

In the mathematical discipline of graph theory, the dual graph of a planar graph G is a graph that has a vertex for each face of G. The dual graph has an edge for each pair of faces in G that are separated from each other by an edge, and a self-loop when the same face appears on both sides of an edge. Thus, each edge e of G has a corresponding dual edge, whose endpoints are the dual vertices corresponding to the faces on either side of e. The definition of the dual depends on the choice of embedding of the graph G, so it is a property of plane graphs rather than planar graphs. For planar graphs generally, there may be multiple dual graphs, depending on the choice of planar embedding of the graph.

Mesh generation is the practice of creating a mesh, a subdivision of a continuous geometric space into discrete geometric and topological cells. Often these cells form a simplicial complex. Usually the cells partition the geometric input domain. Mesh cells are used as discrete local approximations of the larger domain. Meshes are created by computer algorithms, often with human guidance through a GUI, depending on the complexity of the domain and the type of mesh desired. A typical goal is to create a mesh that accurately captures the input domain geometry, with high-quality (well-shaped) cells, and without so many cells as to make subsequent calculations intractable. The mesh should also be fine in areas that are important for the subsequent calculations.
Proximity problems is a class of problems in computational geometry which involve estimation of distances between geometric objects.
Joseph O'Rourke is the Spencer T. and Ann W. Olin Professor of Computer Science at Smith College and the founding chair of the Smith computer science department. His main research interest is computational geometry.
János Pach is a mathematician and computer scientist working in the fields of combinatorics and discrete and computational geometry.
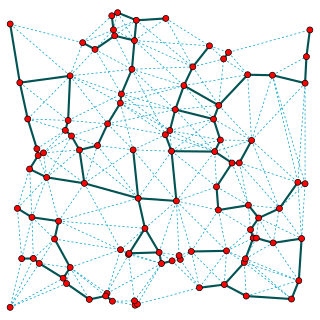
In computational geometry and geometric graph theory, a β-skeleton or beta skeleton is an undirected graph defined from a set of points in the Euclidean plane. Two points p and q are connected by an edge whenever all the angles prq are sharper than a threshold determined from the numerical parameter β.
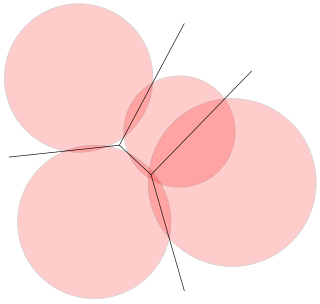
In computational geometry, a power diagram, also called a Laguerre–Voronoi diagram, Dirichlet cell complex, radical Voronoi tesselation or a sectional Dirichlet tesselation, is a partition of the Euclidean plane into polygonal cells defined from a set of circles. The cell for a given circle C consists of all the points for which the power distance to C is smaller than the power distance to the other circles. The power diagram is a form of generalized Voronoi diagram, and coincides with the Voronoi diagram of the circle centers in the case that all the circles have equal radii.
Algorithmic Geometry is a textbook on computational geometry. It was originally written in the French language by Jean-Daniel Boissonnat and Mariette Yvinec, and published as Géometrie algorithmique by Edusciences in 1995. It was translated into English by Hervé Brönnimann, with improvements to some proofs and additional exercises, and published by the Cambridge University Press in 1998.
Davenport–Schinzel Sequences and Their Geometric Applications is a book in discrete geometry. It was written by Micha Sharir and Pankaj K. Agarwal, and published by Cambridge University Press in 1995, with a paperback reprint in 2010.

Geometric and Topological Inference is a monograph in computational geometry, computational topology, geometry processing, and topological data analysis, on the problem of inferring properties of an unknown space from a finite point cloud of noisy samples from the space. It was written by Jean-Daniel Boissonnat, Frédéric Chazal, and Mariette Yvinec, and published in 2018 by the Cambridge University Press in their Cambridge Texts in Applied Mathematics book series. The Basic Library List Committee of the Mathematical Association of America has suggested its inclusion in undergraduate mathematics libraries.
References
- Jacob E. Goodman; Joseph O'Rourke, eds. (2004) [1997]. Handbook of Discrete and Computational Geometry. North-Holland. ISBN 0-8493-8524-5. 1st edition:, 2nd edition: ISBN 1-58488-301-4.
- In its organization, the book resembles the classical handbook in algorithms, Introduction to Algorithms , in its comprehensiveness, only restricted to discrete and computational geometry, computational topology, as well as a broad range of their applications. The second edition expands the book by half, with 14 chapters added and old chapters brought up to date. Its 65 chapters (in over 1,500 pages) are written by a large team of active researchers in the field. [6]
- Jörg-Rudiger Sack; Jorge Urrutia (1998). Handbook of Computational Geometry. North-Holland. ISBN 0-444-82537-1. 1st edition:, 2nd edition (2000): 1-584-88301-4.
- The handbook contains survey chapters in classical and new studies in geometric algorithms: hyperplane arrangements, Voronoi diagrams, geometric and spatial data structures, polygon decomposition, randomized algorithms, derandomization, parallel computational geometry (deterministic and randomized), visibility, Art Gallery and Illumination Problems, closest point problems, link distance problems, similarity of geometric objects, Davenport–Schinzel sequences, spanning trees and spanners for geometric graphs, robustness and numerical issues for geometric algorithms, animation, and graph drawing.
- In addition, the book surveys applications of geometric algorithms in such areas as geographic information systems, geometric shortest path and network optimization and mesh generation.
- Ding-Zhu Du; Frank Hwang (1995). Computing in Euclidean Geometry. Lectures Notes Series on Computing. Vol. 4 (2nd ed.). World Scientific. ISBN 981-02-1876-1.
- "This book is a collection of surveys and exploratory articles about recent developments in the field of computational Euclidean geometry." [7] Its 11 chapters cover quantitative geometry, a history of computational geometry, mesh generation, automated generation of geometric proofs, randomized geometric algorithms, Steiner tree problems, Voronoi diagrams and Delaunay triangulations, constraint solving, spline surfaces, network design, and numerical primitives for geometric computing.