In mathematics, an ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse having both focal points at the same location. The elongation of an ellipse is represented by its eccentricity, which for an ellipse can be any number from 0 to arbitrarily close to but less than 1.

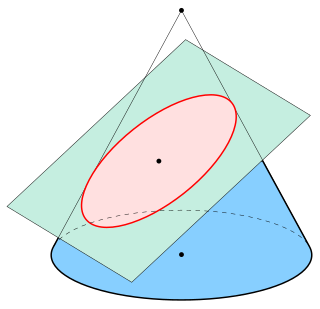
In mathematics, a hyperbola is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, that are mirror images of each other and resemble two infinite bows. The hyperbola is one of the three kinds of conic section, formed by the intersection of a plane and a double cone. If the plane intersects both halves of the double cone but does not pass through the apex of the cones, then the conic is a hyperbola.

A geographic coordinate system is a coordinate system that enables every location on Earth to be specified by a set of numbers, letters or symbols. The coordinates are often chosen such that one of the numbers represents a vertical position and two or three of the numbers represent a horizontal position; alternatively, a geographic position may be expressed in a combined three-dimensional Cartesian vector. A common choice of coordinates is latitude, longitude and elevation. To specify a location on a plane requires a map projection.
In mathematics, curvature is any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object such as a surface deviates from being a flat plane, or a curve from being straight as in the case of a line, but this is defined in different ways depending on the context. There is a key distinction between extrinsic curvature, which is defined for objects embedded in another space – in a way that relates to the radius of curvature of circles that touch the object – and intrinsic curvature, which is defined in terms of the lengths of curves within a Riemannian manifold.

In elementary geometry, the property of being perpendicular (perpendicularity) is the relationship between two lines which meet at a right angle. The property extends to other related geometric objects.
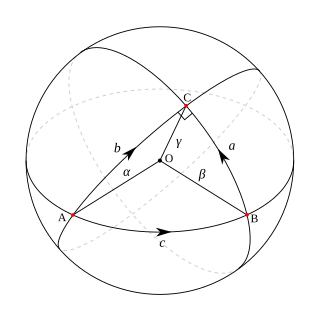
In differential geometry, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". The term "geodesic" comes from geodesy, the science of measuring the size and shape of Earth; in the original sense, a geodesic was the shortest route between two points on the Earth's surface, namely, a segment of a great circle. The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

An ellipsoid is a surface that may be obtained from a sphere by deforming it by means of directional scalings, or more generally, of an affine transformation.
A collider is a type of particle accelerator involving directed beams of particles. Colliders may either be ring accelerators or linear accelerators, and may collide a single beam of particles against a stationary target or two beams head-on.
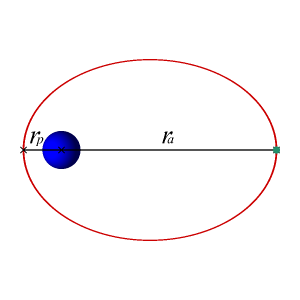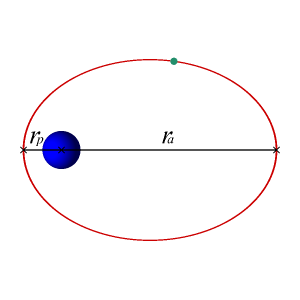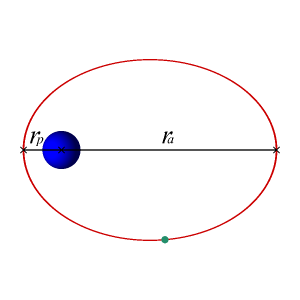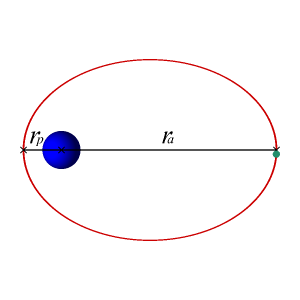
In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.
The Shapiro time delay effect, or gravitational time delay effect, is one of the four classic solar-system tests of general relativity. Radar signals passing near a massive object take slightly longer to travel to a target and longer to return than they would if the mass of the object were not present. The time delay is caused by spacetime dilation, which increases the path length. In an article entitled Fourth Test of General Relativity, astrophysicist Irwin Shapiro wrote:
Because, according to the general theory, the speed of a light wave depends on the strength of the gravitational potential along its path, these time delays should thereby be increased by almost 2×10−4 sec when the radar pulses pass near the sun. Such a change, equivalent to 60 km in distance, could now be measured over the required path length to within about 5 to 10% with presently obtainable equipment.
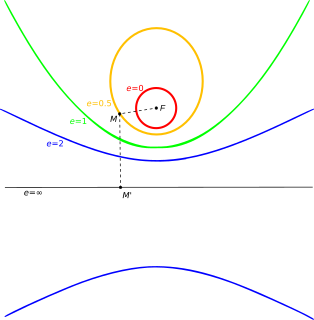
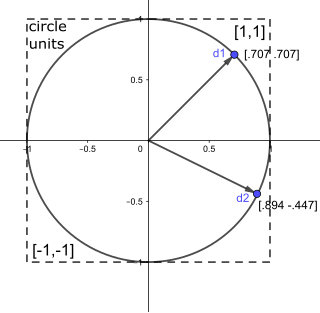
In mathematics, the eccentricity of a conic section is a non-negative real number that uniquely characterizes its shape.
In physics and astronomy, Euler's three-body problem is to solve for the motion of a particle that is acted upon by the gravitational field of two other point masses that are fixed in space. This problem is exactly solvable, and yields an approximate solution for particles moving in the gravitational fields of prolate and oblate spheroids. This problem is named after Leonhard Euler, who discussed it in memoirs published in 1760. Important extensions and analyses were contributed subsequently by Lagrange, Liouville, Laplace, Jacobi, Darboux, Le Verrier, Velde, Hamilton, Poincaré, Birkhoff and E. T. Whittaker, among others.
In optics, an index ellipsoid is a diagram of an ellipsoid that depicts the orientation and relative magnitude of refractive indices in a crystal .

In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga posed and solved this famous problem in his work Ἐπαφαί ; this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets.

The impact parameter is defined as the perpendicular distance between the path of a projectile and the center of a potential field created by an object that the projectile is approaching. It is often referred to in nuclear physics and in classical mechanics.

A great ellipse is an ellipse passing through two points on a spheroid and having the same center as that of the spheroid. Equivalently, it is an ellipse on the surface of a spheroid and centered on the origin, or the curve formed by intersecting the spheroid by a plane through its center. For points that are separated by less than about a quarter of the circumference of the earth, about , the length of the great ellipse connecting the points is close to the geodesic distance.

In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the widest points of the perimeter.
Lamé's stress ellipsoid is an alternative to Mohr's circle for the graphical representation of the stress state at a point. The surface of the ellipsoid represents the locus of the endpoints of all stress vectors acting on all planes passing through a given point in the continuum body. In other words, the endpoints of all stress vectors at a given point in the continuum body lie on the stress ellipsoid surface, i.e., the radius-vector from the center of the ellipsoid, located at the material point in consideration, to a point on the surface of the ellipsoid is equal to the stress vector on some plane passing through the point. In two dimensions, the surface is represented by an ellipse.
A depletion force is an effective attractive force that arises between large colloidal particles that are suspended in a dilute solution of depletants, which are smaller solutes that are preferentially excluded from the vicinity of the large particles. One of the earliest reports of depletion forces that lead to particle coagulation is that of Bondy, who observed the separation or 'creaming' of rubber latex upon addition of polymer depletant molecules to solution. More generally, depletants can include polymers, micelles, osmolytes, ink, mud, or paint dispersed in a continuous phase.