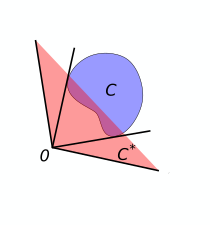
Dual cone and polar cone

A set C and its dual cone C.

A set C and its polar cone C. The dual cone and the polar cone are symmetric to each other with respect to the origin.

Dual cone and polar cone are closely related concepts in convex analysis, a branch of mathematics.

Dual cone

In a vector space

The dual coneC^* of a subset C in a linear space X over the reals, e.g. Euclidean space Rⁿ, with dual space X^* is the set

${\displaystyle C^{*}=\left\{y\in X^{*}:\langle y,x\rangle \geq 0\quad \forall x\in C\right\},}$

where ${\displaystyle \langle y,x\rangle }$ is the duality pairing between X and X^*, i.e. ${\displaystyle \langle y,x\rangle =y(x)}$.

C^* is always a convex cone, even if C is neither convex nor a cone.

In a topological vector space

If X is a topological vector space over the real or complex numbers, then the dual cone of a subset C ⊆ X is the following set of continuous linear functionals on X:

${\displaystyle C^{\prime }:=\left\{f\in X^{\prime }:\operatorname {Re} \left(f(x)\right)\geq 0{\text{ for all }}x\in C\right\}}$, ^[1]

which is the polar of the set -C. ^[1] No matter what C is, ${\displaystyle C^{\prime }}$ will be a convex cone. If C ⊆ {0} then ${\displaystyle C^{\prime }=X^{\prime }}$.

In a Hilbert space (internal dual cone)

Alternatively, many authors define the dual cone in the context of a real Hilbert space (such as Rⁿ equipped with the Euclidean inner product) to be what is sometimes called the internal dual cone.

${\displaystyle C_{\text{internal}}^{*}:=\left\{y\in X:\langle y,x\rangle \geq 0\quad \forall x\in C\right\}.}$

Properties

Using this latter definition for C^*, we have that when C is a cone, the following properties hold: ^[2]

• A non-zero vector y is in C^* if and only if both of the following conditions hold:

1. y is a normal at the origin of a hyperplane that supports C.
2. y and C lie on the same side of that supporting hyperplane.

• C^* is closed and convex.
• ${\displaystyle C_{1}\subseteq C_{2}}$ implies ${\displaystyle C_{2}^{*}\subseteq C_{1}^{*}}$.
• If C has nonempty interior, then C^* is pointed, i.e. C* contains no line in its entirety.
• If C is a cone and the closure of C is pointed, then C^* has nonempty interior.
• C^** is the closure of the smallest convex cone containing C (a consequence of the hyperplane separation theorem)

Self-dual cones

A cone C in a vector space X is said to be self-dual if X can be equipped with an inner product ⟨⋅,⋅⟩ such that the internal dual cone relative to this inner product is equal to C. ^[3] Those authors who define the dual cone as the internal dual cone in a real Hilbert space usually say that a cone is self-dual if it is equal to its internal dual. This is slightly different from the above definition, which permits a change of inner product. For instance, the above definition makes a cone in Rⁿ with ellipsoidal base self-dual, because the inner product can be changed to make the base spherical, and a cone with spherical base in Rⁿ is equal to its internal dual.

The nonnegative orthant of Rⁿ and the space of all positive semidefinite matrices are self-dual, as are the cones with ellipsoidal base (often called "spherical cones", "Lorentz cones", or sometimes "ice-cream cones"). So are all cones in R³ whose base is the convex hull of a regular polygon with an odd number of vertices. A less regular example is the cone in R³ whose base is the "house": the convex hull of a square and a point outside the square forming an equilateral triangle (of the appropriate height) with one of the sides of the square.

Polar cone

The polar of the closed convex cone C is the closed convex cone C, and vice versa.

For a set C in X, the polar cone of C is the set ^[4]

${\displaystyle C^{o}=\left\{y\in X^{*}:\langle y,x\rangle \leq 0\quad \forall x\in C\right\}.}$

It can be seen that the polar cone is equal to the negative of the dual cone, i.e. C^o = −C^*.

For a closed convex cone C in X, the polar cone is equivalent to the polar set for C. ^[5]

See also

• Bipolar theorem
• Polar set

References

1. Schaefer & Wolff 1999, pp. 215–222.
2. Boyd, Stephen P.; Vandenberghe, Lieven (2004). Convex Optimization (pdf). Cambridge University Press. pp. 51–53. ISBN   978-0-521-83378-3 . Retrieved October 15, 2011.
3. Iochum, Bruno, "Cônes autopolaires et algèbres de Jordan", Springer, 1984.
4. Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. pp. 121–122. ISBN   978-0-691-01586-6.
5. Aliprantis, C.D.; Border, K.C. (2007). Infinite Dimensional Analysis: A Hitchhiker's Guide (3 ed.). Springer. p. 215. doi:10.1007/3-540-29587-9. ISBN   978-3-540-32696-0.

Bibliography

• Boltyanski, V. G.; Martini, H.; Soltan, P. (1997). Excursions into combinatorial geometry. New York: Springer. ISBN   3-540-61341-2.
• Goh, C. J.; Yang, X.Q. (2002). Duality in optimization and variational inequalities. London; New York: Taylor & Francis. ISBN   0-415-27479-6.
• Narici, Lawrence; Beckenstein, Edward (2011). Topological Vector Spaces. Pure and applied mathematics (Second ed.). Boca Raton, FL: CRC Press. ISBN   978-1584888666. OCLC   144216834.
• Ramm, A.G. (2000). Shivakumar, P.N.; Strauss, A.V. (eds.). Operator theory and its applications. Providence, R.I.: American Mathematical Society. ISBN   0-8218-1990-9.
• Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN   978-1-4612-7155-0. OCLC   840278135.