
In mechanics, acceleration is the rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are vector quantities. The orientation of an object's acceleration is given by the orientation of the net force acting on that object. The magnitude of an object's acceleration, as described by Newton's Second Law, is the combined effect of two causes:

Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a body, until the discovery of the atom and particle physics. It was found that different atoms and different elementary particles, theoretically with the same amount of matter, have nonetheless different masses. Mass in modern physics has multiple definitions which are conceptually distinct, but physically equivalent. Mass can be experimentally defined as a measure of the body's inertia, meaning the resistance to acceleration when a net force is applied. The object's mass also determines the strength of its gravitational attraction to other bodies.

In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion.

In celestial mechanics, escape velocity or escape speed is the minimum speed needed for an object to escape from contact with or orbit of a primary body, assuming:

In physics, equations of motion are equations that describe the behavior of a physical system in terms of its motion as a function of time. More specifically, the equations of motion describe the behavior of a physical system as a set of mathematical functions in terms of dynamic variables. These variables are usually spatial coordinates and time, but may include momentum components. The most general choice are generalized coordinates which can be any convenient variables characteristic of the physical system. The functions are defined in a Euclidean space in classical mechanics, but are replaced by curved spaces in relativity. If the dynamics of a system is known, the equations are the solutions for the differential equations describing the motion of the dynamics.
In classical mechanics, free fall is any motion of a body where gravity is the only force acting upon it. A freely falling object may not necessarily be falling down in the vertical direction. An object moving upwards might not normally be considered to be falling, but if it is subject to only the force of gravity, it is said to be in free fall. The Moon is thus in free fall around the Earth, though its orbital speed keeps it in very far orbit from the Earth's surface.

A tautochrone curve or isochrone curve is the curve for which the time taken by an object sliding without friction in uniform gravity to its lowest point is independent of its starting point on the curve. The curve is a cycloid, and the time is equal to π times the square root of the radius over the acceleration of gravity. The tautochrone curve is related to the brachistochrone curve, which is also a cycloid.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets, satellites, and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
Newton's law of universal gravitation states that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distance between their centers. Separated objects attract and are attracted as if all their mass were concentrated at their centers. The publication of the law has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.

Terminal velocity is the maximum speed attainable by an object as it falls through a fluid. It is reached when the sum of the drag force (Fd) and the buoyancy is equal to the downward force of gravity (FG) acting on the object. Since the net force on the object is zero, the object has zero acceleration. For objects falling through air at normal pressure, the buoyant force is usually dismissed and not taken into account, as its effects are negligible.
Time dilation is the difference in elapsed time as measured by two clocks, either because of a relative velocity between them, or a difference in gravitational potential between their locations. When unspecified, "time dilation" usually refers to the effect due to velocity.
In classical mechanics, the gravitational potential is a scalar potential associating with each point in space the work per unit mass that would be needed to move an object to that point from a fixed reference point in the conservative gravitational field. It is analogous to the electric potential with mass playing the role of charge. The reference point, where the potential is zero, is by convention infinitely far away from any mass, resulting in a negative potential at any finite distance. Their similarity is correlated with both associated fields having conservative forces.
Gravitational time dilation is a form of time dilation, an actual difference of elapsed time between two events, as measured by observers situated at varying distances from a gravitating mass. The lower the gravitational potential, the slower time passes, speeding up as the gravitational potential increases. Albert Einstein originally predicted this in his theory of relativity, and it has since been confirmed by tests of general relativity.

Projectile motion is a form of motion experienced by an object or particle that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive.
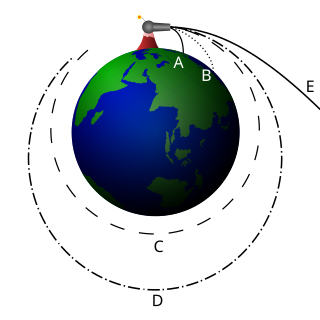
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.
The surface gravity, g, of an astronomical object is the gravitational acceleration experienced at its surface at the equator, including the effects of rotation. The surface gravity may be thought of as the acceleration due to gravity experienced by a hypothetical test particle which is very close to the object's surface and which, in order not to disturb the system, has negligible mass. For objects where the surface is deep in the atmosphere and the radius not known, the surface gravity is given at the 1 bar pressure level in the atmosphere.

A gravity train is a theoretical means of transportation for purposes of commuting between two points on the surface of a sphere, by following a straight tunnel connecting the two points through the interior of the sphere.

The gravity of Earth, denoted by g, is the net acceleration that is imparted to objects due to the combined effect of gravitation and the centrifugal force . It is a vector quantity, whose direction coincides with a plumb bob and strength or magnitude is given by the norm .

Velocity is the speed in combination with the direction of motion of an object. Velocity is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of bodies.









































