
The Navier–Stokes equations are partial differential equations which describe the motion of viscous fluid substances. They were named after French engineer and physicist Claude-Louis Navier and the Irish physicist and mathematician George Gabriel Stokes. They were developed over several decades of progressively building the theories, from 1822 (Navier) to 1842–1850 (Stokes).
In Newtonian physics, free fall is any motion of a body where gravity is the only force acting upon it. In the context of general relativity, where gravitation is reduced to a space-time curvature, a body in free fall has no force acting on it.

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets, satellites, and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and the law of universal gravitation. Orbital mechanics is a core discipline within space-mission design and control.
In gravitationally bound systems, the orbital speed of an astronomical body or object is the speed at which it orbits around either the barycenter or, if one body is much more massive than the other bodies of the system combined, its speed relative to the center of mass of the most massive body.
A Newtonian fluid is a fluid in which the viscous stresses arising from its flow are at every point linearly correlated to the local strain rate — the rate of change of its deformation over time. Stresses are proportional to the rate of change of the fluid's velocity vector.

A sub-orbital spaceflight is a spaceflight in which the spacecraft reaches outer space, but its trajectory intersects the surface of the gravitating body from which it was launched. Hence, it will not complete one orbital revolution, will not become an artificial satellite nor will it reach escape velocity.

Projectile motion is a form of motion experienced by an object or particle that is projected in a gravitational field, such as from Earth's surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive and negligible. The curved path of objects in projectile motion was shown by Galileo to be a parabola, but may also be a straight line in the special case when it is thrown directly upward or downward. The study of such motions is called ballistics, and such a trajectory is a ballistic trajectory. The only force of mathematical significance that is actively exerted on the object is gravity, which acts downward, thus imparting to the object a downward acceleration towards the Earth’s center of mass. Because of the object's inertia, no external force is needed to maintain the horizontal velocity component of the object's motion. Taking other forces into account, such as aerodynamic drag or internal propulsion, requires additional analysis. A ballistic missile is a missile only guided during the relatively brief initial powered phase of flight, and whose remaining course is governed by the laws of classical mechanics.
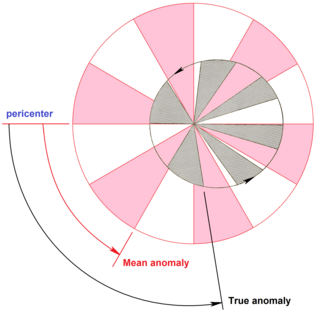
In celestial mechanics, the mean anomaly is the fraction of an elliptical orbit's period that has elapsed since the orbiting body passed periapsis, expressed as an angle which can be used in calculating the position of that body in the classical two-body problem. It is the angular distance from the pericenter which a fictitious body would have if it moved in a circular orbit, with constant speed, in the same orbital period as the actual body in its elliptical orbit.

In astrodynamics or celestial mechanics a parabolic trajectory is a Kepler orbit with the eccentricity equal to 1 and is an unbound orbit that is exactly on the border between elliptical and hyperbolic. When moving away from the source it is called an escape orbit, otherwise a capture orbit. It is also sometimes referred to as a C3 = 0 orbit (see Characteristic energy).

In astrodynamics or celestial mechanics, a hyperbolic trajectory or hyperbolic orbit is the trajectory of any object around a central body with more than enough speed to escape the central object's gravitational pull. The name derives from the fact that according to Newtonian theory such an orbit has the shape of a hyperbola. In more technical terms this can be expressed by the condition that the orbital eccentricity is greater than one.

In astrodynamics or celestial mechanics, an elliptic orbit or elliptical orbit is a Kepler orbit with an eccentricity of less than 1; this includes the special case of a circular orbit, with eccentricity equal to 0. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1. In a wider sense, it is a Kepler orbit with negative energy. This includes the radial elliptic orbit, with eccentricity equal to 1.
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle. In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version.
In celestial mechanics, the specific relative angular momentum of a body is the angular momentum of that body divided by its mass. In the case of two orbiting bodies it is the vector product of their relative position and relative linear momentum, divided by the mass of the body in question.
In the gravitational two-body problem, the specific orbital energy of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy, divided by the reduced mass. According to the orbital energy conservation equation, it does not vary with time:
In astrodynamics, an orbit equation defines the path of orbiting body around central body relative to , without specifying position as a function of time. Under standard assumptions, a body moving under the influence of a force, directed to a central body, with a magnitude inversely proportional to the square of the distance, has an orbit that is a conic section with the central body located at one of the two foci, or the focus.
In general relativity, Schwarzschild geodesics describe the motion of test particles in the gravitational field of a central fixed mass that is, motion in the Schwarzschild metric. Schwarzschild geodesics have been pivotal in the validation of Einstein's theory of general relativity. For example, they provide accurate predictions of the anomalous precession of the planets in the Solar System and of the deflection of light by gravity.

Spacecraft flight dynamics is the application of mechanical dynamics to model how the external forces acting on a space vehicle or spacecraft determine its flight path. These forces are primarily of three types: propulsive force provided by the vehicle's engines; gravitational force exerted by the Earth and other celestial bodies; and aerodynamic lift and drag.

In astronautics and aerospace engineering, the bi-elliptic transfer is an orbital maneuver that moves a spacecraft from one orbit to another and may, in certain situations, require less delta-v than a Hohmann transfer maneuver.
In orbital mechanics, the universal variable formulation is a method used to solve the two-body Kepler problem. It is a generalized form of Kepler's Equation, extending them to apply not only to elliptic orbits, but also parabolic and hyperbolic orbits. It thus is applicable to many situations in the Solar System, where orbits of widely varying eccentricities are present.
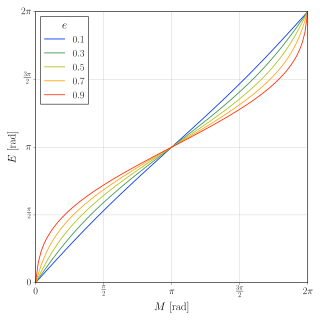
In orbital mechanics, Kepler's equation relates various geometric properties of the orbit of a body subject to a central force.






























