 | This article needs additional citations for verification .(March 2017) |
In astrology, the equatorial ascendant, or the East point, is the sign and degree rising over the Eastern Horizon at the Earth's equator at any given time. In the celestial sphere it corresponds to the intersection of the ecliptic with a great circle containing the ecliptic poles and the East point of the horizon.
Equations derived from spherical trigonometry allow for the conversion from equatorial coordinates to ecliptic coordinates. As points in the ecliptic have no latitude (β=0º) and the East point of the horizon has a right ascension 6h higher than that of the meridian (or 90º more in hour angle), the equation that determines East Point's longitude can be written as:
where is the local sidereal time and is the obliquity of the ecliptic. [1] The equation can also be derived from the Ascendant at the equator (=0º).
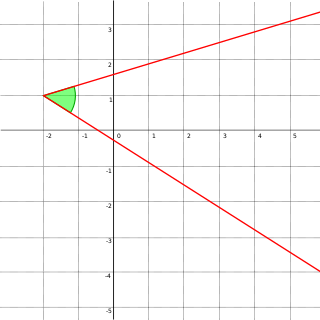
In Euclidean geometry, an angle is the figure formed by two rays, called the sides of the angle, sharing a common endpoint, called the vertex of the angle. Angles formed by two rays are also known as plane angles as they lie in the plane that contains the rays. Angles are also formed by the intersection of two planes; these are called dihedral angles. Two intersecting curves may also define an angle, which is the angle of the rays lying tangent to the respective curves at their point of intersection.
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x, one has where e is the base of the natural logarithm, i is the imaginary unit, and cos and sin are the trigonometric functions cosine and sine respectively. This complex exponential function is sometimes denoted cis x. The formula is still valid if x is a complex number, and is also called Euler's formula in this more general case.
In geography, latitude is a coordinate that specifies the north–south position of a point on the surface of the Earth or another celestial body. Latitude is given as an angle that ranges from −90° at the south pole to 90° at the north pole, with 0° at the Equator. Lines of constant latitude, or parallels, run east–west as circles parallel to the equator. Latitude and longitude are used together as a coordinate pair to specify a location on the surface of the Earth.
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a given point in space is specified by three real numbers: the radial distancer along the radial line connecting the point to the fixed point of origin; the polar angleθ between the radial line and a given polar axis; and the azimuthal angleφ as the angle of rotation of the radial line around the polar axis. (See graphic regarding the "physics convention".) Once the radius is fixed, the three coordinates (r, θ, φ), known as a 3-tuple, provide a coordinate system on a sphere, typically called the spherical polar coordinates. The plane passing through the origin and perpendicular to the polar axis (where the polar angle is a right angle) is called the reference plane (sometimes fundamental plane).
In mathematics, the trigonometric functions are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis.
The propagation constant of a sinusoidal electromagnetic wave is a measure of the change undergone by the amplitude and phase of the wave as it propagates in a given direction. The quantity being measured can be the voltage, the current in a circuit, or a field vector such as electric field strength or flux density. The propagation constant itself measures the dimensionless change in magnitude or phase per unit length. In the context of two-port networks and their cascades, propagation constant measures the change undergone by the source quantity as it propagates from one port to the next.
In astronomy, coordinate systems are used for specifying positions of celestial objects relative to a given reference frame, based on physical reference points available to a situated observer. Coordinate systems in astronomy can specify an object's relative position in three-dimensional space or plot merely by its direction on a celestial sphere, if the object's distance is unknown or trivial.
In mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering. The calculation of mathematical tables was an important area of study, which led to the development of the first mechanical computing devices.
The ascendant or rising sign is the astrological sign on the eastern horizon when the person was born. It signifies a person's physical appearance, and awakening consciousness.
The equation of time describes the discrepancy between two kinds of solar time. The word equation is used in the medieval sense of "reconciliation of a difference". The two times that differ are the apparent solar time, which directly tracks the diurnal motion of the Sun, and mean solar time, which tracks a theoretical mean Sun with uniform motion along the celestial equator. Apparent solar time can be obtained by measurement of the current position of the Sun, as indicated by a sundial. Mean solar time, for the same place, would be the time indicated by a steady clock set so that over the year its differences from apparent solar time would have a mean of zero.
The Mollweide projection is an equal-area, pseudocylindrical map projection generally used for maps of the world or celestial sphere. It is also known as the Babinet projection, homalographic projection, homolographic projection, and elliptical projection. The projection trades accuracy of angle and shape for accuracy of proportions in area, and as such is used where that property is needed, such as maps depicting global distributions.
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations between the sine and cosine functions.
For small angles, the trigonometric functions sine, cosine, and tangent can be calculated with reasonable accuracy by the following simple approximations:
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system.
Rifleman's rule is a "rule of thumb" that allows a rifleman to accurately fire a rifle that has been calibrated for horizontal targets at uphill or downhill targets. The rule says that only the horizontal range should be considered when adjusting a sight or performing hold-over in order to account for bullet drop. Typically, the range of an elevated target is considered in terms of the slant range, incorporating both the horizontal distance and the elevation distance, as when a rangefinder is used to determine the distance to target. The slant range is not compatible with standard ballistics tables for estimating bullet drop.
A pendulum is a body suspended from a fixed support such that it freely swings back and forth under the influence of gravity. When a pendulum is displaced sideways from its resting, equilibrium position, it is subject to a restoring force due to gravity that will accelerate it back towards the equilibrium position. When released, the restoring force acting on the pendulum's mass causes it to oscillate about the equilibrium position, swinging it back and forth. The mathematics of pendulums are in general quite complicated. Simplifying assumptions can be made, which in the case of a simple pendulum allow the equations of motion to be solved analytically for small-angle oscillations.
In geometry and computer graphics, a supertoroid or supertorus is usually understood to be a family of doughnut-like surfaces whose shape is defined by mathematical formulas similar to those that define the superellipsoids. The plural of "supertorus" is either supertori or supertoruses.
The Bowring series of the transverse mercator published in 1989 by Bernard Russel Bowring gave formulas for the Transverse Mercator that are simpler to program but retain millimeter accuracy.
The table of chords, created by the Greek astronomer, geometer, and geographer Ptolemy in Egypt during the 2nd century AD, is a trigonometric table in Book I, chapter 11 of Ptolemy's Almagest, a treatise on mathematical astronomy. It is essentially equivalent to a table of values of the sine function. It was the earliest trigonometric table extensive enough for many practical purposes, including those of astronomy. Since the 8th and 9th centuries, the sine and other trigonometric functions have been used in Islamic mathematics and astronomy, reforming the production of sine tables. Khwarizmi and Habash al-Hasib later produced a set of trigonometric tables.
The position of the Sun in the sky is a function of both the time and the geographic location of observation on Earth's surface. As Earth orbits the Sun over the course of a year, the Sun appears to move with respect to the fixed stars on the celestial sphere, along a circular path called the ecliptic.
 | This astrology-related article is a stub. You can help Wikipedia by expanding it. |
