
In mathematics, a field is a set on which addition, subtraction, multiplication, and division are defined and behave as the corresponding operations on rational and real numbers. A field is thus a fundamental algebraic structure which is widely used in algebra, number theory, and many other areas of mathematics.

In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word isomorphism is derived from the Ancient Greek: ἴσοςisos "equal", and μορφήmorphe "form" or "shape".

In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" when reaching a certain value, called the modulus. The modern approach to modular arithmetic was developed by Carl Friedrich Gauss in his book Disquisitiones Arithmeticae, published in 1801.
In algebra, the kernel of a homomorphism is generally the inverse image of 0. An important special case is the kernel of a linear map. The kernel of a matrix, also called the null space, is the kernel of the linear map defined by the matrix.
In abstract algebra, a congruence relation is an equivalence relation on an algebraic structure that is compatible with the structure in the sense that algebraic operations done with equivalent elements will yield equivalent elements. Every congruence relation has a corresponding quotient structure, whose elements are the equivalence classes for the relation.

In mathematics, the free groupFS over a given set S consists of all words that can be built from members of S, considering two words to be different unless their equality follows from the group axioms. The members of S are called generators of FS, and the number of generators is the rank of the free group. An arbitrary group G is called free if it is isomorphic to FS for some subset S of G, that is, if there is a subset S of G such that every element of G can be written in exactly one way as a product of finitely many elements of S and their inverses.
In mathematics, equality is a relationship between two quantities or, more generally, two mathematical expressions, asserting that the quantities have the same value, or that the expressions represent the same mathematical object. Equality between A and B is written A = B, and pronounced "A equals B". The symbol "=" is called an "equals sign". Two objects that are not equal are said to be distinct.
In number theory, the ideal class group of an algebraic number field K is the quotient group JK /PK where JK is the group of fractional ideals of the ring of integers of K, and PK is its subgroup of principal ideals. The class group is a measure of the extent to which unique factorization fails in the ring of integers of K. The order of the group, which is finite, is called the class number of K.

In graph theory, an isomorphism of graphsG and H is a bijection between the vertex sets of G and H
In mathematics and logic, the term "uniqueness" refers to the property of being the one and only object satisfying a certain condition. This sort of quantification is known as uniqueness quantification or unique existential quantification, and is often denoted with the symbols "∃!" or "∃=1". For example, the formal statement
In category theory, a branch of abstract mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics. Establishing an equivalence involves demonstrating strong similarities between the mathematical structures concerned. In some cases, these structures may appear to be unrelated at a superficial or intuitive level, making the notion fairly powerful: it creates the opportunity to "translate" theorems between different kinds of mathematical structures, knowing that the essential meaning of those theorems is preserved under the translation.
In homotopy theory, the Whitehead theorem states that if a continuous mapping f between CW complexes X and Y induces isomorphisms on all homotopy groups, then f is a homotopy equivalence. This result was proved by J. H. C. Whitehead in two landmark papers from 1949, and provides a justification for working with the concept of a CW complex that he introduced there. It is a model result of algebraic topology, in which the behavior of certain algebraic invariants determines a topological property of a mapping.
In mathematics, categorification is the process of replacing set-theoretic theorems with category-theoretic analogues. Categorification, when done successfully, replaces sets with categories, functions with functors, and equations with natural isomorphisms of functors satisfying additional properties. The term was coined by Louis Crane.
In mathematics, the Grothendieck group, or group of differences, of a commutative monoid M is a certain abelian group. This abelian group is constructed from M in the most universal way, in the sense that any abelian group containing a homomorphic image of M will also contain a homomorphic image of the Grothendieck group of M. The Grothendieck group construction takes its name from a specific case in category theory, introduced by Alexander Grothendieck in his proof of the Grothendieck–Riemann–Roch theorem, which resulted in the development of K-theory. This specific case is the monoid of isomorphism classes of objects of an abelian category, with the direct sum as its operation.
In mathematics, a skeleton of a category is a subcategory that, roughly speaking, does not contain any extraneous isomorphisms. In a certain sense, the skeleton of a category is the "smallest" equivalent category, which captures all "categorical properties" of the original. In fact, two categories are equivalent if and only if they have isomorphic skeletons. A category is called skeletal if isomorphic objects are necessarily identical.
Abstract analytic number theory is a branch of mathematics which takes the ideas and techniques of classical analytic number theory and applies them to a variety of different mathematical fields. The classical prime number theorem serves as a prototypical example, and the emphasis is on abstract asymptotic distribution results. The theory was invented and developed by mathematicians such as John Knopfmacher and Arne Beurling in the twentieth century.

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann. The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.
In mathematics, an approximately finite-dimensional (AF) C*-algebra is a C*-algebra that is the inductive limit of a sequence of finite-dimensional C*-algebras. Approximate finite-dimensionality was first defined and described combinatorially by Ola Bratteli. Later, George A. Elliott gave a complete classification of AF algebras using the K0 functor whose range consists of ordered abelian groups with sufficiently nice order structure.
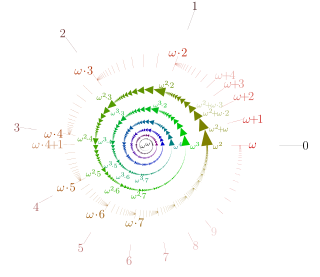
In set theory, an ordinal number, or ordinal, is a generalization of ordinal numerals aimed to extend enumeration to infinite sets.
In order theory and model theory, branches of mathematics, Cantor's isomorphism theorem states that every two countable dense unbounded linear orders are order-isomorphic. For instance, Minkowski's question-mark function produces an isomorphism between the numerical ordering of the rational numbers and the numerical ordering of the dyadic rationals.













