
In physics, mathematics, engineering, and related fields, a wave is a propagating dynamic disturbance of one or more quantities. Periodic waves oscillate repeatedly about an equilibrium (resting) value at some frequency. When the entire waveform moves in one direction, it is said to be a travelling wave; by contrast, a pair of superimposed periodic waves traveling in opposite directions makes a standing wave. In a standing wave, the amplitude of vibration has nulls at some positions where the wave amplitude appears smaller or even zero. Waves are often described by a wave equation or a one-way wave equation for single wave propagation in a defined direction.

In physics and electrical engineering, a cutoff frequency, corner frequency, or break frequency is a boundary in a system's frequency response at which energy flowing through the system begins to be reduced rather than passing through.

In fluid dynamics, gravity waves are waves generated in a fluid medium or at the interface between two media when the force of gravity or buoyancy tries to restore equilibrium. An example of such an interface is that between the atmosphere and the ocean, which gives rise to wind waves.
In fluid dynamics, Stokes' law is an empirical law for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a viscous fluid. It was derived by George Gabriel Stokes in 1851 by solving the Stokes flow limit for small Reynolds numbers of the Navier–Stokes equations.

In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to – the Debye T 3 law. Similarly to the Einstein photoelectron model, it recovers the Dulong–Petit law at high temperatures. Due to simplifying assumptions, its accuracy suffers at intermediate temperatures.

Stellar dynamics is the branch of astrophysics which describes in a statistical way the collective motions of stars subject to their mutual gravity. The essential difference from celestial mechanics is that the number of body
Plasma oscillations, also known as Langmuir waves, are rapid oscillations of the electron density in conducting media such as plasmas or metals in the ultraviolet region. The oscillations can be described as an instability in the dielectric function of a free electron gas. The frequency depends only weakly on the wavelength of the oscillation. The quasiparticle resulting from the quantization of these oscillations is the plasmon.

In applied mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element.

In quantum mechanics, a two-state system is a quantum system that can exist in any quantum superposition of two independent quantum states. The Hilbert space describing such a system is two-dimensional. Therefore, a complete basis spanning the space will consist of two independent states. Any two-state system can also be seen as a qubit.

The Rayleigh–Taylor instability, or RT instability, is an instability of an interface between two fluids of different densities which occurs when the lighter fluid is pushing the heavier fluid. Examples include the behavior of water suspended above oil in the gravity of Earth, mushroom clouds like those from volcanic eruptions and atmospheric nuclear explosions, supernova explosions in which expanding core gas is accelerated into denser shell gas, instabilities in plasma fusion reactors and inertial confinement fusion.

Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case corresponding to small deflections of a beam that is subjected to lateral loads only. By ignoring the effects of shear deformation and rotatory inertia, it is thus a special case of Timoshenko–Ehrenfest beam theory. It was first enunciated circa 1750, but was not applied on a large scale until the development of the Eiffel Tower and the Ferris wheel in the late 19th century. Following these successful demonstrations, it quickly became a cornerstone of engineering and an enabler of the Second Industrial Revolution.
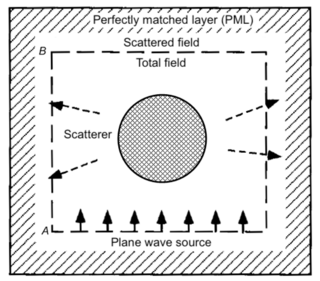
A perfectly matched layer (PML) is an artificial absorbing layer for wave equations, commonly used to truncate computational regions in numerical methods to simulate problems with open boundaries, especially in the FDTD and FE methods. The key property of a PML that distinguishes it from an ordinary absorbing material is that it is designed so that waves incident upon the PML from a non-PML medium do not reflect at the interface—this property allows the PML to strongly absorb outgoing waves from the interior of a computational region without reflecting them back into the interior.
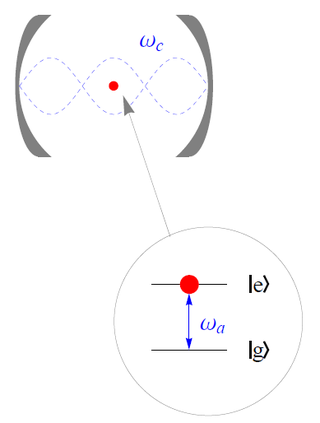
The Jaynes–Cummings model is a theoretical model in quantum optics. It describes the system of a two-level atom interacting with a quantized mode of an optical cavity, with or without the presence of light. It was originally developed to study the interaction of atoms with the quantized electromagnetic field in order to investigate the phenomena of spontaneous emission and absorption of photons in a cavity.

Inertial waves, also known as inertial oscillations, are a type of mechanical wave possible in rotating fluids. Unlike surface gravity waves commonly seen at the beach or in the bathtub, inertial waves flow through the interior of the fluid, not at the surface. Like any other kind of wave, an inertial wave is caused by a restoring force and characterized by its wavelength and frequency. Because the restoring force for inertial waves is the Coriolis force, their wavelengths and frequencies are related in a peculiar way. Inertial waves are transverse. Most commonly they are observed in atmospheres, oceans, lakes, and laboratory experiments. Rossby waves, geostrophic currents, and geostrophic winds are examples of inertial waves. Inertial waves are also likely to exist in the molten core of the rotating Earth.
Atmospheric tides are global-scale periodic oscillations of the atmosphere. In many ways they are analogous to ocean tides. They can be excited by:
The McCumber relation is a relationship between the effective cross-sections of absorption and emission of light in the physics of solid-state lasers. It is named after Dean McCumber, who proposed the relationship in 1964.

In fluid dynamics, a Stokes wave is a nonlinear and periodic surface wave on an inviscid fluid layer of constant mean depth. This type of modelling has its origins in the mid 19th century when Sir George Stokes – using a perturbation series approach, now known as the Stokes expansion – obtained approximate solutions for nonlinear wave motion.
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational. This theory was first published, in correct form, by George Biddell Airy in the 19th century.
In the physics of continuous media, spatial dispersion is usually described as a phenomenon where material parameters such as permittivity or conductivity have dependence on wavevector. Normally, such a dependence is assumed to be absent for simplicity, however spatial dispersion exists to varying degrees in all materials.
In quantum computing, Mølmer–Sørensen gate scheme refers to an implementation procedure for various multi-qubit quantum logic gates used mostly in trapped ion quantum computing. This procedure is based on the original proposition by Klaus Mølmer and Anders Sørensen in 1999-2000.




































