 |
In mathematics, the generalized dihedral groups are a family of groups with algebraic structures similar to that of the dihedral groups. They include the finite dihedral groups, the infinite dihedral group, and the orthogonal group O(2). Dihedral groups play an important role in group theory, geometry, and chemistry.
For any abelian group H, the generalized dihedral group of H, written Dih(H), is the semidirect product of H and Z2, with Z2 acting on H by inverting elements. I.e., with φ(0) the identity and φ(1) inversion.
Thus we get:
for all h1, h2 in H and t2 in Z2.
(Writing Z2 multiplicatively, we have (h1, t1) * (h2, t2) = (h1 + t1h2, t1t2) .)
Note that (h, 0) * (0,1) = (h,1), i.e. first the inversion and then the operation in H. Also (0, 1) * (h, t) = (−h, 1 + t); indeed (0,1) inverts h, and toggles t between "normal" (0) and "inverted" (1) (this combined operation is its own inverse).
The subgroup of Dih(H) of elements (h, 0) is a normal subgroup of index 2, isomorphic to H, while the elements (h, 1) are all their own inverse.
The conjugacy classes are:
Thus for every subgroup M of H, the corresponding set of elements (m,0) is also a normal subgroup. We have:
Dih(H) is Abelian, with the semidirect product a direct product, if and only if all elements of H are their own inverse, i.e., an elementary abelian 2-group:
etc.
Dih(Rn ) and its dihedral subgroups are disconnected topological groups. Dih(Rn ) consists of two connected components: the identity component isomorphic to Rn, and the component with the reflections. Similarly O(2) consists of two connected components: the identity component isomorphic to the circle group, and the component with the reflections.
For the group Dih∞ we can distinguish two cases:
Both topological groups are totally disconnected, but in the first case the (singleton) components are open, while in the second case they are not. Also, the first topological group is a closed subgroup of Dih(R) but the second is not a closed subgroup of O(2).
In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is mapped to itself by every automorphism of the parent group. Because every conjugation map is an inner automorphism, every characteristic subgroup is normal; though the converse is not guaranteed. Examples of characteristic subgroups include the commutator subgroup and the center of a group.
In mathematics, specifically group theory, given a prime number p, a p-group is a group in which the order of every element is a power of p. That is, for each element g of a p-group G, there exists a nonnegative integer n such that the product of pn copies of g, and not fewer, is equal to the identity element. The orders of different elements may be different powers of p.
In group theory, the symmetry group of a geometric object is the group of all transformations under which the object is invariant, endowed with the group operation of composition. Such a transformation is an invertible mapping of the ambient space which takes the object to itself, and which preserves all the relevant structure of the object. A frequent notation for the symmetry group of an object X is G = Sym(X).
In mathematics, specifically in group theory, the concept of a semidirect product is a generalization of a direct product. There are two closely related concepts of semidirect product:
In mathematics, a dihedral group is the group of symmetries of a regular polygon, which includes rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.
In group theory, a dicyclic group (notation Dicn or Q4n, ⟨n,2,2⟩) is a particular kind of non-abelian group of order 4n (n > 1). It is an extension of the cyclic group of order 2 by a cyclic group of order 2n, giving the name di-cyclic. In the notation of exact sequences of groups, this extension can be expressed as:
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. The orthogonal group is sometimes called the general orthogonal group, by analogy with the general linear group. Equivalently, it is the group of orthogonal matrices, where the group operation is given by matrix multiplication. The orthogonal group is an algebraic group and a Lie group. It is compact.
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of that root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection group. In fact it turns out that most finite reflection groups are Weyl groups. Abstractly, Weyl groups are finite Coxeter groups, and are important examples of these.
In mathematics, a group extension is a general means of describing a group in terms of a particular normal subgroup and quotient group. If and are two groups, then is an extension of by if there is a short exact sequence
In mathematics, a topological group G is called a discrete group if there is no limit point in it. Equivalently, the group G is discrete if and only if its identity is isolated.
In mathematics, a Euclidean group is the group of (Euclidean) isometries of a Euclidean space ; that is, the transformations of that space that preserve the Euclidean distance between any two points (also called Euclidean transformations). The group depends only on the dimension n of the space, and is commonly denoted E(n) or ISO(n).
In mathematics, a covering group of a topological group H is a covering space G of H such that G is a topological group and the covering map p : G → H is a continuous group homomorphism. The map p is called the covering homomorphism. A frequently occurring case is a double covering group, a topological double cover in which H has index 2 in G; examples include the spin groups, pin groups, and metaplectic groups.
In mathematics, the pin group is a certain subgroup of the Clifford algebra associated to a quadratic space. It maps 2-to-1 to the orthogonal group, just as the spin group maps 2-to-1 to the special orthogonal group.
A one-dimensional symmetry group is a mathematical group that describes symmetries in one dimension (1D).
In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O(3), the group of all isometries that leave the origin fixed, or correspondingly, the group of orthogonal matrices. O(3) itself is a subgroup of the Euclidean group E(3) of all isometries.
A regular tetrahedron has 12 rotational symmetries, and a symmetry order of 24 including transformations that combine a reflection and a rotation.
In a group, the conjugate by g of h is ghg−1.
In geometry, a two-dimensional point group or rosette group is a group of geometric symmetries (isometries) that keep at least one point fixed in a plane. Every such group is a subgroup of the orthogonal group O(2), including O(2) itself. Its elements are rotations and reflections, and every such group containing only rotations is a subgroup of the special orthogonal group SO(2), including SO(2) itself. That group is isomorphic to R/Z and the first unitary group, U(1), a group also known as the circle group.
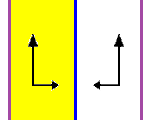
In mathematics, the infinite dihedral group Dih∞ is an infinite group with properties analogous to those of the finite dihedral groups.
