Gray graph

Gray graph
Gray graph
	The Gray graph
Named after	Marion Cameron Gray
Vertices	54
Edges	81
Radius	6
Diameter	6
Girth	8
Automorphisms	1296
Chromatic number	2
Chromatic index	3
Genus	7
Book thickness	3
Queue number	2
Properties	Cubic ; Semi-symmetric ; Hamiltonian ; Bipartite
	Table of graphs and parameters

Last updated December 28, 2023

In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive (see below).

Construction

3 × 3 × 3 grid whose point-line incidences are described by the Gray graph

Graph with vertices arranged and colored by their position in the grid

Graph as a unit-distance graph with 3-fold rotational symmetry

The Gray graph can be constructed ( Bouwer 1972 ) from the 27 points of a 3 × 3 × 3 grid and the 27 axis-parallel lines through these points. This collection of points and lines forms a projective configuration: each point has exactly three lines through it, and each line has exactly three points on it. The Gray graph is the Levi graph of this configuration; it has a vertex for every point and every line of the configuration, and an edge for every pair of a point and a line that touch each other. This construction generalizes (Bouwer 1972) to any dimension n ≥ 3, yielding an n-valent Levi graph with algebraic properties similar to those of the Gray graph. In (Monson, Pisanski, Schulte, Ivic-Weiss 2007), the Gray graph appears as a different sort of Levi graph for the edges and triangular faces of a certain locally toroidal abstract regular 4-polytope. It is therefore the first in an infinite family of similarly constructed cubic graphs. As with other Levi graphs, it is a bipartite graph, with the vertices corresponding to points on one side of the bipartition and the vertices corresponding to lines on the other side.

Marušič and Pisanski (2000) give several alternative methods of constructing the Gray graph. As with any bipartite graph, there are no odd-length cycles, and there are also no cycles of four or six vertices, so the girth of the Gray graph is 8. The simplest oriented surface on which the Gray graph can be embedded has genus 7 ( Marušič, Pisanski & Wilson 2005 ).

The Gray graph is Hamiltonian and can be constructed from the LCF notation:

[-25,7,-7,13,-13,25]^{9}.\

As a Hamiltonian cubic graph, it has chromatic index three.

Algebraic properties

The automorphism group of the Gray graph is a group of order 1296. It acts transitively on the edges the graph but not on its vertices: there are symmetries taking every edge to any other edge, but not taking every vertex to any other vertex. The vertices that correspond to points of the underlying configuration can only be symmetric to other vertices that correspond to points, and the vertices that correspond to lines can only be symmetric to other vertices that correspond to lines. Therefore, the Gray graph is a semi-symmetric graph, the smallest possible cubic semi-symmetric graph.

The characteristic polynomial of the Gray graph is

(x-3)x^{16}(x+3)(x^{2}-6)^{6}(x^{2}-3)^{12}.\

Geometric properties

The Gray graph can be represented by points in the plane in such a way that adjacent vertices are at unit distance apart; that is, it is a unit distance graph. ^[1]

Related Research Articles

Dragan Marušič is a Slovene mathematician. Marušič obtained his BSc in technical mathematics from the University of Ljubljana in 1976, and his PhD from the University of Reading in 1981 under the supervision of Crispin Nash-Williams.

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

In the mathematical field of graph theory, an edge-transitive graph is a graph $G$ such that, given any two edges $e 1$ and $e 2$ of $G$ , there is an automorphism of $G$ that maps $e 1$ to $e 2$ .

<span class="mw-page-title-main">Incidence structure</span> Abstract mathematical system of two types of objects and a relation between them

In mathematics, an incidence structure is an abstract system consisting of two types of objects and a single relationship between these types of objects. Consider the points and lines of the Euclidean plane as the two types of objects and ignore all the properties of this geometry except for the relation of which points are on which lines for all points and lines. What is left is the incidence structure of the Euclidean plane.

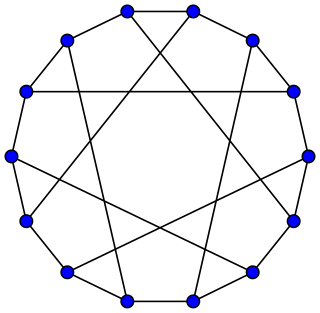
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.

In the mathematical field of graph theory, the Tutte–Coxeter graph or Tutte eight-cage or Cremona–Richmond graph is a 3-regular graph with 30 vertices and 45 edges. As the unique smallest cubic graph of girth 8, it is a cage and a Moore graph. It is bipartite, and can be constructed as the Levi graph of the generalized quadrangle W₂. The graph is named after William Thomas Tutte and H. S. M. Coxeter; it was discovered by Tutte (1947) but its connection to geometric configurations was investigated by both authors in a pair of jointly published papers.

In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.

<span class="mw-page-title-main">Desargues graph</span> Distance-transitive cubic graph with 20 nodes and 30 edges

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

In the mathematical field of graph theory, a semi-symmetric graph is an undirected graph that is edge-transitive and regular, but not vertex-transitive. In other words, a graph is semi-symmetric if each vertex has the same number of incident edges, and there is a symmetry taking any of the graph's edges to any other of its edges, but there is some pair of vertices such that no symmetry maps the first into the second.

In geometry, the Desargues configuration is a configuration of ten points and ten lines, with three points per line and three lines per point. It is named after Girard Desargues.

In the mathematical field of graph theory, the Pappus graph is a bipartite, 3-regular, undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic, distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

In graph theory, the bipartite double cover of an undirected graph $G$ is a bipartite, covering graph of $G$ , with twice as many vertices as $G$ . It can be constructed as the tensor product of graphs, $G \times K 2$ . It is also called the Kronecker double cover, canonical double cover or simply the bipartite double of $G$ .

In the mathematical field of graph theory, the Folkman graph is a 4-regular graph with 20 vertices and 40 edges. It is a regular bipartite graph with symmetries taking every edge to every other edge, but the two sides of its bipartition are not symmetric with each other, making it the smallest possible semi-symmetric graph. It is named after Jon Folkman, who constructed it for this property in 1967.

In the mathematical field of graph theory, the Nauru graph is a symmetric, bipartite, cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges, rediscovered in 2002 and named after Ljubljana.

In the mathematical field of graph theory, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by H. S. M. Coxeter and Robert Frucht, for the representation of cubic graphs that contain a Hamiltonian cycle. The cycle itself includes two out of the three adjacencies for each vertex, and the LCF notation specifies how far along the cycle each vertex's third neighbor is. A single graph may have multiple different representations in LCF notation.

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges. It is named after W. T. Tutte.

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.

The 110-vertex Iofinova–Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.

References

Bouwer, I. Z. (1968), "An edge but not vertex transitive cubic graph", Canadian Mathematical Bulletin , 11 (4): 533–535, doi: 10.4153/CMB-1968-063-0 . (Izak Zurk Bouwer (1933–2012) was a UNB professor. "Obituary. Izak Bouwer". Ottawa Citizen. December 28, 2012.)
Bouwer, I. Z. (1972), "On edge but not vertex transitive regular graphs", Journal of Combinatorial Theory, Series B, 12: 32–40, doi:10.1016/0095-8956(72)90030-5 .
Folkman, J. (1967), "Regular line-symmetric graphs", Journal of Combinatorial Theory , 3 (3): 533–535, doi: 10.1016/S0021-9800(67)80069-3 .
Marušič, Dragan; Pisanski, Tomaž (2000), "The Gray graph revisited", Journal of Graph Theory , 35: 1–7, doi:10.1002/1097-0118(200009)35:1<1::AID-JGT1>3.0.CO;2-7 .
Marušič, Dragan; Pisanski, Tomaž; Wilson, Steve (2005), "The genus of the Gray graph is 7", European Journal of Combinatorics , 26 (3–4): 377–385, doi: 10.1016/j.ejc.2004.01.015 .
Monson, B.; Pisanski, T.; Schulte, E.; Ivic-Weiss, A. (2007), "Semisymmetric Graphs from Polytopes", Journal of Combinatorial Theory, Series A, 114 (3): 421–435, arXiv: math/0606469 , doi: 10.1016/j.jcta.2006.06.007 , S2CID 10203794

External links

↑ Berman, Leah; Gévay, Gábor; Pisanski, Tomaž (2023). "The Gray graph is a unit-distance graph". arXiv: 2312.15336 ..

This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

[1] Berman, Leah; Gévay, Gábor; Pisanski, Tomaž (2023). "The Gray graph is a unit-distance graph". arXiv: 2312.15336 ..

[1]