In the mathematical field of graph theory, a semi-symmetric graph is an undirected graph that is edge-transitive and regular, but not vertex-transitive. In other words, a graph is semi-symmetric if each vertex has the same number of incident edges, and there is a symmetry taking any of the graph's edges to any other of its edges, but there is some pair of vertices such that no symmetry maps the first into the second.
A semi-symmetric graph must be bipartite, and its automorphism group must act transitively on each of the two vertex sets of the bipartition (in fact, regularity is not required for this property to hold). For instance, in the diagram of the Folkman graph shown here, green vertices can not be mapped to red ones by any automorphism, but every two vertices of the same color are symmetric with each other.
Semi-symmetric graphs were first studied E. Dauber, a student of F. Harary, in a paper, no longer available, titled "On line- but not point-symmetric graphs". This was seen by Jon Folkman, whose paper, published in 1967, includes the smallest semi-symmetric graph, now known as the Folkman graph, on 20 vertices. [1] The term "semi-symmetric" was first used by Klin et al. in a paper they published in 1978. [2]
The smallest cubic semi-symmetric graph (that is, one in which each vertex is incident to exactly three edges) is the Gray graph on 54 vertices. It was first observed to be semi-symmetric by Bouwer (1968). It was proven to be the smallest cubic semi-symmetric graph by Dragan Marušič and Aleksander Malnič. [3]
All the cubic semi-symmetric graphs on up to 768 vertices are known. According to Conder, Malnič, Marušič and Potočnik, the four smallest possible cubic semi-symmetric graphs after the Gray graph are the Iofinova–Ivanov graph on 110 vertices, the Ljubljana graph on 112 vertices, [4] a graph on 120 vertices with girth 8 and the Tutte 12-cage. [5]
Dragan Marušič is a Slovene mathematician. Marušič obtained his BSc in technical mathematics from the University of Ljubljana in 1976, and his PhD from the University of Reading in 1981 under the supervision of Crispin Nash-Williams.
In the mathematical field of graph theory, a vertex-transitive graph is a graph G in which, given any two vertices v1 and v2 of G, there is some automorphism
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is an automorphism of G that maps e1 to e2.
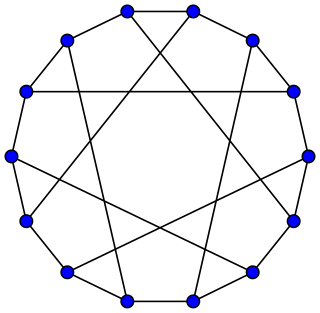
In the mathematical field of graph theory, the Heawood graph is an undirected graph with 14 vertices and 21 edges, named after Percy John Heawood.
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.
In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphism
In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive.
In the mathematical field of graph theory, the Pappus graph is a bipartite 3-regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek mathematician who is believed to have discovered the "hexagon theorem" describing the Pappus configuration. All the cubic distance-regular graphs are known; the Pappus graph is one of the 13 such graphs.
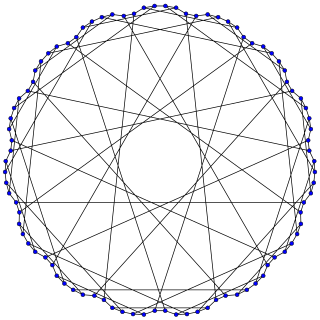
In the mathematical field of graph theory, the Foster graph is a bipartite 3-regular graph with 90 vertices and 135 edges.
In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.
In the mathematical field of graph theory, the Folkman graph, named after Jon Folkman, is a bipartite 4-regular graph with 20 vertices and 40 edges.
In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.
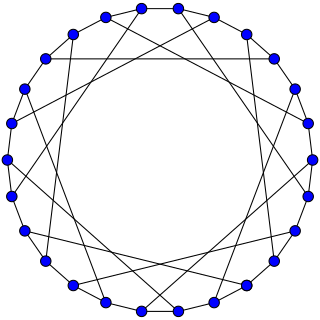
In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.
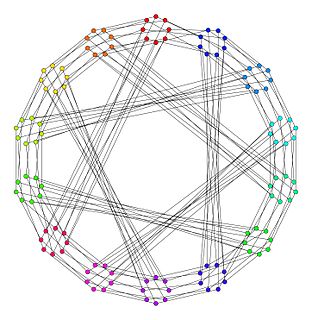
In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.
In graph theory, the Holt graph or Doyle graph is the smallest half-transitive graph, that is, the smallest example of a vertex-transitive and edge-transitive graph which is not also symmetric. Such graphs are not common. It is named after Peter G. Doyle and Derek F. Holt, who discovered the same graph independently in 1976 and 1981 respectively.
In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges named after W. T. Tutte.
In the mathematical field of graph theory, the Klein graphs are two different but related regular graphs, each with 84 edges. Each can be embedded in the orientable surface of genus 3, in which they form dual graphs.
In the mathematical field of graph theory, the Dejter graph is a 6-regular graph with 112 vertices and 336 edges. The Dejter graph is obtained by deleting a copy of the Hamming code of length 7 from the binary 7-cube.
In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.
The 110-vertex Iofinova-Ivanov graph is, in graph theory, a semi-symmetric cubic graph with 110 vertices and 165 edges.
{{cite journal}}: Cite journal requires |journal= (help)