
In mathematics, an alternating group is the group of even permutations of a finite set. The alternating group on a set of n elements is called the alternating group of degree n, or the alternating group on n letters and denoted by An or Alt(n).

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges.

In mathematics, random graph is the general term to refer to probability distributions over graphs. Random graphs may be described simply by a probability distribution, or by a random process which generates them. The theory of random graphs lies at the intersection between graph theory and probability theory. From a mathematical perspective, random graphs are used to answer questions about the properties of typical graphs. Its practical applications are found in all areas in which complex networks need to be modeled – many random graph models are thus known, mirroring the diverse types of complex networks encountered in different areas. In a mathematical context, random graph refers almost exclusively to the Erdős–Rényi random graph model. In other contexts, any graph model may be referred to as a random graph.
In the mathematical field of graph theory, an automorphism is a permutation of the vertices such that edges are mapped to edges and non-edges are mapped to non-edges. A graph is a vertex-transitive graph if, given any two vertices v1 and v2 of G, there is an automorphism f such that

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

In the mathematical field of graph theory, a graph G is symmetric if, given any two pairs of adjacent vertices u1—v1 and u2—v2 of G, there is an automorphism

In the mathematical field of graph theory, the Desargues graph is a distance-transitive, cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements that need to be removed to separate the remaining nodes into two or more isolated subgraphs. It is closely related to the theory of network flow problems. The connectivity of a graph is an important measure of its resilience as a network.

In mathematics, Paley graphs are undirected graphs constructed from the members of a suitable finite field by connecting pairs of elements that differ by a quadratic residue. The Paley graphs form an infinite family of conference graphs, which yield an infinite family of symmetric conference matrices. Paley graphs allow graph-theoretic tools to be applied to the number theory of quadratic residues, and have interesting properties that make them useful in graph theory more generally.

In the mathematical field of graph theory, the Rado graph, Erdős–Rényi graph, or random graph is a countably infinite graph that can be constructed by choosing independently at random for each pair of its vertices whether to connect the vertices by an edge. The names of this graph honor Richard Rado, Paul Erdős, and Alfréd Rényi, mathematicians who studied it in the early 1960s; it appears even earlier in the work of Wilhelm Ackermann. The Rado graph can also be constructed non-randomly, by symmetrizing the membership relation of the hereditarily finite sets, by applying the BIT predicate to the binary representations of the natural numbers, or as an infinite Paley graph that has edges connecting pairs of prime numbers congruent to 1 mod 4 that are quadratic residues modulo each other.

In the mathematical field of graph theory, the Erdős–Rényi model refers to one of two closely related models for generating random graphs or the evolution of a random network. These models are named after Hungarian mathematicians Paul Erdős and Alfréd Rényi, who introduced one of the models in 1959. Edgar Gilbert introduced the other model contemporaneously with and independently of Erdős and Rényi. In the model of Erdős and Rényi, all graphs on a fixed vertex set with a fixed number of edges are equally likely. In the model introduced by Gilbert, also called the Erdős–Rényi–Gilbert model, each edge has a fixed probability of being present or absent, independently of the other edges. These models can be used in the probabilistic method to prove the existence of graphs satisfying various properties, or to provide a rigorous definition of what it means for a property to hold for almost all graphs.

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.
In the mathematical field of graph theory, an automorphism of a graph is a form of symmetry in which the graph is mapped onto itself while preserving the edge–vertex connectivity.
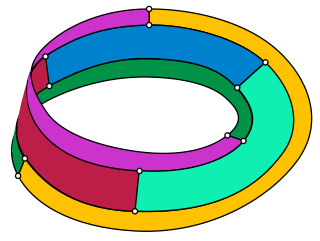
In the mathematical field of graph theory, Tietze's graph is an undirected cubic graph with 12 vertices and 18 edges. It is named after Heinrich Franz Friedrich Tietze, who showed in 1910 that the Möbius strip can be subdivided into six regions that all touch each other – three along the boundary of the strip and three along its center line – and therefore that graphs that are embedded onto the Möbius strip may require six colors. The boundary segments of the regions of Tietze's subdivision form an embedding of Tietze's graph.

In the mathematical field of graph theory, the Frucht graph is a cubic graph with 12 vertices, 18 edges, and no nontrivial symmetries. It was first described by Robert Frucht in 1939.

In the mathematical field of graph theory, the Nauru graph is a symmetric, bipartite, cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.
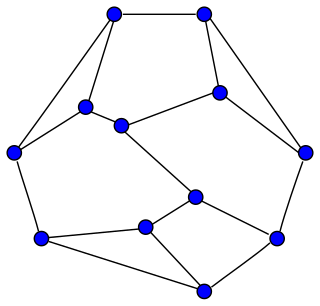
Frucht's theorem is a result in algebraic graph theory, conjectured by Dénes Kőnig in 1936 and proved by Robert Frucht in 1939. It states that every finite group is the group of symmetries of a finite undirected graph. More strongly, for any finite group G there exist infinitely many non-isomorphic simple connected graphs such that the automorphism group of each of them is isomorphic to G.

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge.
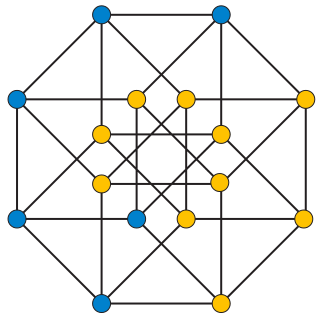
In graph theory, a distinguishing coloring or distinguishing labeling of a graph is an assignment of colors or labels to the vertices of the graph that destroys all of the nontrivial symmetries of the graph. The coloring does not need to be a proper coloring: adjacent vertices are allowed to be given the same color. For the colored graph, there should not exist any one-to-one mapping of the vertices to themselves that preserves both adjacency and coloring. The minimum number of colors in a distinguishing coloring is called the distinguishing number of the graph.
















