In graph-theoretic mathematics, a biregular graph [1] or semiregular bipartite graph [2] is a bipartite graph for which every two vertices on the same side of the given bipartition have the same degree as each other. If the degree of the vertices in is and the degree of the vertices in is , then the graph is said to be -biregular.
Every complete bipartite graph is -biregular. [3] The rhombic dodecahedron is another example; it is (3,4)-biregular. [4]
An -biregular graph must satisfy the equation . This follows from a simple double counting argument: the number of endpoints of edges in is , the number of endpoints of edges in is , and each edge contributes the same amount (one) to both numbers.
Every regular bipartite graph is also biregular. Every edge-transitive graph (disallowing graphs with isolated vertices) that is not also vertex-transitive must be biregular. [3] In particular every edge-transitive graph is either regular or biregular.
The Levi graphs of geometric configurations are biregular; a biregular graph is the Levi graph of an (abstract) configuration if and only if its girth is at least six. [5]
In mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of vertices which are connected by edges. A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically; see Graph for more detailed definitions and for other variations in the types of graph that are commonly considered. Graphs are one of the prime objects of study in discrete mathematics.
In mathematics, a hypergraph is a generalization of a graph in which an edge can join any number of vertices. In contrast, in an ordinary graph, an edge connects exactly two vertices. Formally, a hypergraph is a pair where is a set of elements called nodes or vertices, and is a set of non-empty subsets of called hyperedges or edges. Therefore, is a subset of , where is the power set of . The size of the vertex set is called the order of the hypergraph, and the size of edges set is the size of the hypergraph.
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets and such that every edge connects a vertex in to one in . Vertex sets and are usually called the parts of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles.
In graph theory and computer science, an adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.
This is a glossary of graph theory terms. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by edges.
In mathematics, and more specifically in graph theory, a graph is a structure amounting to a set of objects in which some pairs of the objects are in some sense "related". The objects correspond to mathematical abstractions called vertices and each of the related pairs of vertices is called an edge. Typically, a graph is depicted in diagrammatic form as a set of dots or circles for the vertices, joined by lines or curves for the edges. Graphs are one of the objects of study in discrete mathematics.
In graph theory, two graphs and are homeomorphic if there is a graph isomorphism from some subdivision of to some subdivision of . If the edges of a graph are thought of as lines drawn from one vertex to another, then two graphs are homeomorphic to each other in the graph-theoretic sense precisely if they are homeomorphic in the sense in which the term is used in topology.
In the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is an automorphism of G that maps e1 to e2.
In the mathematical discipline of graph theory, the line graph of an undirected graph G is another graph L(G) that represents the adjacencies between edges of G. L(G) is constructed in the following way: for each edge in G, make a vertex in L(G); for every two edges in G that have a vertex in common, make an edge between their corresponding vertices in L(G).
In graph theory, a branch of mathematics, list coloring is a type of graph coloring where each vertex can be restricted to a list of allowed colors. It was first studied in the 1970s in independent papers by Vizing and by Erdős, Rubin, and Taylor.
In the mathematical theory of matroids, a graphic matroid is a matroid whose independent sets are the forests in a given finite undirected graph. The dual matroids of graphic matroids are called co-graphic matroids or bond matroids. A matroid that is both graphic and co-graphic is called a planar matroid; these are exactly the graphic matroids formed from planar graphs.
In graph theory, the degree of a vertex of a graph is the number of edges that are incident to the vertex, and in a multigraph, loops are counted twice. The degree of a vertex is denoted or . The maximum degree of a graph , denoted by , and the minimum degree of a graph, denoted by , are the maximum and minimum degree of its vertices. In the multigraph on the right, the maximum degree is 5 and the minimum degree is 0.
In combinatorial mathematics, a Levi graph or incidence graph is a bipartite graph associated with an incidence structure. From a collection of points and lines in an incidence geometry or a projective configuration, we form a graph with one vertex per point, one vertex per line, and an edge for every incidence between a point and a line. They are named for Friedrich Wilhelm Levi, who wrote about them in 1942.
In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive.
In the mathematical area of graph theory, Kőnig's theorem, proved by Dénes Kőnig (1931), describes an equivalence between the maximum matching problem and the minimum vertex cover problem in bipartite graphs. It was discovered independently, also in 1931, by Jenő Egerváry in the more general case of weighted graphs.
In graph theory, a rook's graph is a graph that represents all legal moves of the rook chess piece on a chessboard. Each vertex of a rook's graph represents a square on a chessboard, and each edge represents a legal move from one square to another. The same graphs can be defined mathematically as the Cartesian products of two complete graphs or as the line graphs of complete bipartite graphs.
In mathematics, a permutation graph is a graph whose vertices represent the elements of a permutation, and whose edges represent pairs of elements that are reversed by the permutation. Permutation graphs may also be defined geometrically, as the intersection graphs of line segments whose endpoints lie on two parallel lines. Different permutations may give rise to the same permutation graph; a given graph has a unique representation if it is prime with respect to the modular decomposition.
In matroid theory, a field within mathematics, a gammoid is a certain kind of matroid, describing sets of vertices that can be reached by vertex-disjoint paths in a directed graph.
In graph theory, the modular decomposition is a decomposition of a graph into subsets of vertices called modules. A module is a generalization of a connected component of a graph. Unlike connected components, however, one module can be a proper subset of another. Modules therefore lead to a recursive (hierarchical) decomposition of the graph, instead of just a partition.
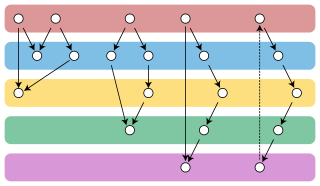
In graph theory, the Gallai–Hasse–Roy–Vitaver theorem is a form of duality between the colorings of the vertices of a given undirected graph and the orientations of its edges. It states that the minimum number of colors needed to properly color any graph G equals one plus the length of a longest path in an orientation of G chosen to minimize this path's length. The orientations for which the longest path has minimum length always include at least one acyclic orientation.
