Zero-symmetric graph

Last updated
18-vertex zero-symmetric graph.svg
The smallest zero-symmetric graph, with 18 vertices and 27 edges
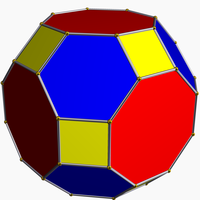
Great rhombicuboctahedron.png
The truncated cuboctahedron, a zero-symmetric polyhedron
Graph families defined by their automorphisms
distance-transitive → distance-regular ← strongly regular
↓
symmetric (arc-transitive) ← t-transitive,t ≥ 2 skew-symmetric
↓
(if connected)
vertex- and edge-transitive 		→ edge-transitive and regular → edge-transitive
↓↓↓
vertex-transitive → regular →(if bipartite)
biregular
↑
Cayley graph ← zero-symmetric asymmetric

In the mathematical field of graph theory, a zero-symmetric graph is a connected graph in which each vertex has exactly three incident edges and, for each two vertices, there is a unique symmetry taking one vertex to the other. Such a graph is a vertex-transitive graph but cannot be an edge-transitive graph: the number of symmetries equals the number of vertices, too few to take every edge to every other edge. [1]

Contents

The smallest zero-symmetric graph with two edge orbits Two-edge-orbit GRR.svg
The smallest zero-symmetric graph with two edge orbits

The name for this class of graphs was coined by R. M. Foster in a 1966 letter to H. S. M. Coxeter. [2] In the context of group theory, zero-symmetric graphs are also called graphical regular representations of their symmetry groups. [3]

Examples

The smallest zero-symmetric graph is a nonplanar graph with 18 vertices. [4] Its LCF notation is [5,−5]9.

Among planar graphs, the truncated cuboctahedral and truncated icosidodecahedral graphs are also zero-symmetric. [5]

These examples are all bipartite graphs. However, there exist larger examples of zero-symmetric graphs that are not bipartite. [6]

These examples also have three different symmetry classes (orbits) of edges. However, there exist zero-symmetric graphs with only two orbits of edges. The smallest such graph has 20 vertices, with LCF notation [6,6,-6,-6]5. [7]

Properties

Every finite zero-symmetric graph is a Cayley graph, a property that does not always hold for cubic vertex-transitive graphs more generally and that helps in the solution of combinatorial enumeration tasks concerning zero-symmetric graphs. There are 97687 zero-symmetric graphs on up to 1280 vertices. These graphs form 89% of the cubic Cayley graphs and 88% of all connected vertex-transitive cubic graphs on the same number of vertices. [8]

Unsolved problem in mathematics:

Does every finite zero-symmetric graph contain a Hamiltonian cycle?

(more unsolved problems in mathematics)

All known finite connected zero-symmetric graphs contain a Hamiltonian cycle, but it is unknown whether every finite connected zero-symmetric graph is necessarily Hamiltonian. [9] This is a special case of the Lovász conjecture that (with five known exceptions, none of which is zero-symmetric) every finite connected vertex-transitive graph and every finite Cayley graph is Hamiltonian.

See also

Related Research Articles

Petersen graph Cubic graph with 10 vertices and 15 edges

In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three-edge-coloring.

Hamiltonian path Path in a graph that visits each vertex exactly once

In the mathematical field of graph theory, a Hamiltonian path is a path in an undirected or directed graph that visits each vertex exactly once. A Hamiltonian cycle is a Hamiltonian path that is a cycle. Determining whether such paths and cycles exist in graphs is the Hamiltonian path problem, which is NP-complete.

In the mathematical field of graph theory, a vertex-transitive graph is a graph G in which, given any two vertices v1 and v2 of G, there is some automorphism

Cubic graph

In the mathematical field of graph theory, a cubic graph is a graph in which all vertices have degree three. In other words, a cubic graph is a 3-regular graph. Cubic graphs are also called trivalent graphs.

Desargues graph

In the mathematical field of graph theory, the Desargues graph is a distance-transitive cubic graph with 20 vertices and 30 edges. It is named after Girard Desargues, arises from several different combinatorial constructions, has a high level of symmetry, is the only known non-planar cubic partial cube, and has been applied in chemical databases.

Semi-symmetric graph

In the mathematical field of graph theory, a semi-symmetric graph is an undirected graph that is edge-transitive and regular, but not vertex-transitive. In other words, a graph is semi-symmetric if each vertex has the same number of incident edges, and there is a symmetry taking any of the graph's edges to any other of its edges, but there is some pair of vertices such that no symmetry maps the first into the second.

Gray graph

In the mathematical field of graph theory, the Gray graph is an undirected bipartite graph with 54 vertices and 81 edges. It is a cubic graph: every vertex touches exactly three edges. It was discovered by Marion C. Gray in 1932 (unpublished), then discovered independently by Bouwer 1968 in reply to a question posed by Jon Folkman 1967. The Gray graph is interesting as the first known example of a cubic graph having the algebraic property of being edge but not vertex transitive.

In graph theory, the Lovász conjecture (1969) is a classical problem on Hamiltonian paths in graphs. It says:

Coxeter graph

In the mathematical field of graph theory, the Coxeter graph is a 3-regular graph with 28 vertices and 42 edges. It is one of the 13 known cubic distance-regular graphs. It is named after Harold Scott MacDonald Coxeter.

Möbius–Kantor graph

In the mathematical field of graph theory, the Möbius–Kantor graph is a symmetric bipartite cubic graph with 16 vertices and 24 edges named after August Ferdinand Möbius and Seligmann Kantor. It can be defined as the generalized Petersen graph G(8,3): that is, it is formed by the vertices of an octagon, connected to the vertices of an eight-point star in which each point of the star is connected to the points three steps away from it.

Generalized Petersen graph

In graph theory, the generalized Petersen graphs are a family of cubic graphs formed by connecting the vertices of a regular polygon to the corresponding vertices of a star polygon. They include the Petersen graph and generalize one of the ways of constructing the Petersen graph. The generalized Petersen graph family was introduced in 1950 by H. S. M. Coxeter and was given its name in 1969 by Mark Watkins.

Frucht graph

In the mathematical field of graph theory, the Frucht graph is a 3-regular graph with 12 vertices, 18 edges, and no nontrivial symmetries. It was first described by Robert Frucht in 1939.

Nauru graph

In the mathematical field of graph theory, the Nauru graph is a symmetric bipartite cubic graph with 24 vertices and 36 edges. It was named by David Eppstein after the twelve-pointed star in the flag of Nauru.

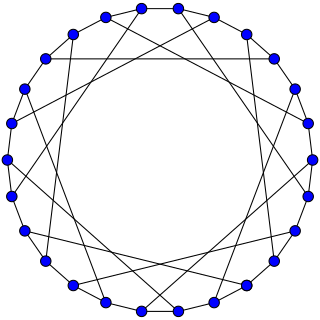
F26A graph

In the mathematical field of graph theory, the F26A graph is a symmetric bipartite cubic graph with 26 vertices and 39 edges.

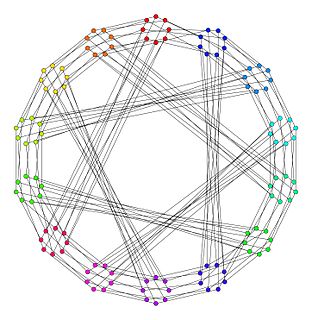
Ljubljana graph

In the mathematical field of graph theory, the Ljubljana graph is an undirected bipartite graph with 112 vertices and 168 edges.

LCF notation

In combinatorial mathematics, LCF notation or LCF code is a notation devised by Joshua Lederberg, and extended by H. S. M. Coxeter and Robert Frucht, for the representation of cubic graphs that contain a Hamiltonian cycle. The cycle itself includes two out of the three adjacencies for each vertex, and the LCF notation specifies how far along the cycle each vertex's third neighbor is. A single graph may have multiple different representations in LCF notation.

Tutte 12-cage

In the mathematical field of graph theory, the Tutte 12-cage or Benson graph is a 3-regular graph with 126 vertices and 189 edges named after W. T. Tutte.

Robert Wertheimer Frucht was a German-Chilean mathematician; his research specialty was graph theory and the symmetries of graphs.

Barnette's conjecture is an unsolved problem in graph theory, a branch of mathematics, concerning Hamiltonian cycles in graphs. It is named after David W. Barnette, a professor emeritus at the University of California, Davis; it states that every bipartite polyhedral graph with three edges per vertex has a Hamiltonian cycle.

The connected 3-regular (cubic) simple graphs are listed for small vertex numbers.

References

  1. ↑ Coxeter, Harold Scott MacDonald; Frucht, Roberto; Powers, David L. (1981), Zero-symmetric graphs, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York-London, ISBN   0-12-194580-4, MR   0658666
  2. ↑ Coxeter, Frucht & Powers (1981), p. ix.
  3. ↑ Lauri, Josef; Scapellato, Raffaele (2003), Topics in Graph Automorphisms and Reconstruction, London Mathematical Society Student Texts, Cambridge University Press, p. 66, ISBN   9780521529037 .
  4. ↑ Coxeter, Frucht & Powers (1981), Figure 1.1, p. 5.
  5. ↑ Coxeter, Frucht & Powers (1981), pp. 75 and 80.
  6. ↑ Coxeter, Frucht & Powers (1981), p. 55.
  7. ↑ Conder, Marston D. E.; Pisanski, Tomaž; Žitnik, Arjana (2017), "Vertex-transitive graphs and their arc-types", Ars Mathematica Contemporanea, 12 (2): 383–413, arXiv: 1505.02029 , doi:10.26493/1855-3974.1146.f96, MR   3646702
  8. ↑ Potočnik, Primož; Spiga, Pablo; Verret, Gabriel (2013), "Cubic vertex-transitive graphs on up to 1280 vertices", Journal of Symbolic Computation, 50: 465–477, arXiv: 1201.5317 , doi:10.1016/j.jsc.2012.09.002, MR   2996891 .
  9. ↑ Coxeter, Frucht & Powers (1981), p. 10.
This page is based on this Wikipedia article
Text is available under the CC BY-SA 4.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.