
Harald G. Niederreiter (born June 7, 1944) is an Austrian mathematician known for his work in discrepancy theory, algebraic geometry, quasi-Monte Carlo methods, and cryptography.

Harald G. Niederreiter (born June 7, 1944) is an Austrian mathematician known for his work in discrepancy theory, algebraic geometry, quasi-Monte Carlo methods, and cryptography.
Niederreiter was born on June 7, 1944, in Vienna, and grew up in Salzburg. [1] [2] He began studying mathematics at the University of Vienna in 1963, [1] [2] and finished his doctorate there in 1969, with a thesis on discrepancy in compact abelian groups supervised by Edmund Hlawka. [3] He began his academic career as an assistant professor at the University of Vienna, but soon moved to Southern Illinois University. [1] [2] During this period he also visited the University of Illinois at Urbana-Champaign, Institute for Advanced Study, and University of California, Los Angeles. [2] In 1978 he moved again, becoming the head of a new mathematics department at the University of the West Indies in Jamaica. In 1981 he returned to Austria for a post at the Austrian Academy of Sciences, where from 1989 to 2000 he served as director of the Institutes of Information Processing and Discrete Mathematics. In 2001 he became a professor at the National University of Singapore. [1] [2] In 2009 he returned to Austria again, to the Johann Radon Institute for Computational and Applied Mathematics of the Austrian Academy of Sciences. He also worked from 2010 to 2011 as a professor at the King Fahd University of Petroleum and Minerals in Saudi Arabia. [2]
Niederreiter's initial research interests were in the abstract algebra of abelian groups and finite fields, subjects also represented by his later book Finite Fields (with Rudolf Lidl, 1983). [1] From his doctoral thesis onwards, he also incorporated discrepancy theory and the theory of uniformly distributed sets in metric spaces into his study of these subjects. [2]
In 1970, Niederreiter began to work on numerical analysis and random number generation, and in 1974 he published the book Uniform Distribution of Sequences. Combining his work on pseudorandom numbers with the Monte Carlo method, he did pioneering research in the quasi-Monte Carlo method in the late 1970s, and again later published a book on the topic, Random Number Generation and Quasi-Monte Carlo Methods (1995). [1] [2]
Niederreiter's interests in pseudorandom numbers also led him to study stream ciphers in the 1980s, and this interest branched out into other areas of cryptography such as public key cryptography. The Niederreiter cryptosystem, an encryption system based on error-correcting codes that can also be used for digital signatures, was developed by him in 1986. [1] His work in cryptography is represented by his book Algebraic Geometry in Coding Theory and Cryptography (with C. P. Xing, 2009). [2]
Returning to pure mathematics, Niederreiter has also made contributions to algebraic geometry with the discovery of many dense curves over finite fields, [1] and published the book Rational Points on Curves over Finite Fields: Theory and Applications (with C. P. Xing, 2001). [2]
Niederreiter is a member of the Austrian Academy of Sciences and the German Academy of Sciences Leopoldina. In 1998 he was an invited speaker at the International Congress of Mathematicians, [4] and won the Kardinal Innitzer Prize. [1] [2] He became a fellow of the American Mathematical Society in 2013. [2]
Niederreiter's book Random Number Generation and Quasi-Monte Carlo Methods won the Outstanding Simulation Publication Award. [1]
In 2014, a workshop in honor of Niederreiter's 70th birthday was held at the Johann Radon Institute for Computational and Applied Mathematics of the Austrian Academy of Sciences, [5] and a Festschrift was published in his honor. [6]

Discrete mathematics is the study of mathematical structures that can be considered "discrete" rather than "continuous". Objects studied in discrete mathematics include integers, graphs, and statements in logic. By contrast, discrete mathematics excludes topics in "continuous mathematics" such as real numbers, calculus or Euclidean geometry. Discrete objects can often be enumerated by integers; more formally, discrete mathematics has been characterized as the branch of mathematics dealing with countable sets. However, there is no exact definition of the term "discrete mathematics".
A pseudorandom sequence of numbers is one that appears to be statistically random, despite having been produced by a completely deterministic and repeatable process. Simply put, the problem is that many of the sources of randomness available to humans rely on physical processes not readily available to computer programs.

In abstract algebra, group theory studies the algebraic structures known as groups. The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces, can all be seen as groups endowed with additional operations and axioms. Groups recur throughout mathematics, and the methods of group theory have influenced many parts of algebra. Linear algebraic groups and Lie groups are two branches of group theory that have experienced advances and have become subject areas in their own right.
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures.
In mathematics, a low-discrepancy sequence is a sequence with the property that for all values of N, its subsequence x1, ..., xN has a low discrepancy.

In numerical analysis, the quasi-Monte Carlo method is a method for numerical integration and solving some other problems using low-discrepancy sequences to achieve variance reduction. This is in contrast to the regular Monte Carlo method or Monte Carlo integration, which are based on sequences of pseudorandom numbers.
In mathematics, Diophantine geometry is the study of Diophantine equations by means of powerful methods in algebraic geometry. By the 20th century it became clear for some mathematicians that methods of algebraic geometry are ideal tools to study these equations. Diophantine geometry is part of the broader field of arithmetic geometry.
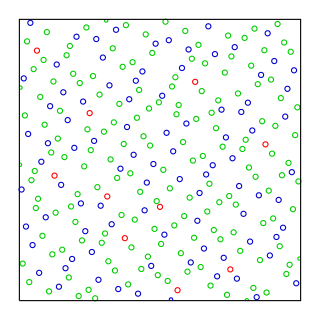
In statistics, Halton sequences are sequences used to generate points in space for numerical methods such as Monte Carlo simulations. Although these sequences are deterministic, they are of low discrepancy, that is, appear to be random for many purposes. They were first introduced in 1960 and are an example of a quasi-random number sequence. They generalize the one-dimensional van der Corput sequences.

Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act.
Vladimir Gershonovich Drinfeld, surname also romanized as Drinfel'd, is a renowned mathematician from the former USSR, who emigrated to the United States and is currently working at the University of Chicago.
Hasse's theorem on elliptic curves, also referred to as the Hasse bound, provides an estimate of the number of points on an elliptic curve over a finite field, bounding the value both above and below.

Michael Artin is a German-American mathematician and a professor emeritus in the Massachusetts Institute of Technology Mathematics Department, known for his contributions to algebraic geometry.
Inversive congruential generators are a type of nonlinear congruential pseudorandom number generator, which use the modular multiplicative inverse to generate the next number in a sequence. The standard formula for an inversive congruential generator, modulo some prime q is:
In coding theory, the Singleton bound, named after Richard Collom Singleton, is a relatively crude upper bound on the size of an arbitrary block code with block length , size and minimum distance . It is also known as the Joshibound. proved by Joshi (1958) and even earlier by Komamiya (1953).
In mathematics, a multivariate polynomial defined over the rational numbers is absolutely irreducible if it is irreducible over the complex field. For example, is absolutely irreducible, but while is irreducible over the integers and the reals, it is reducible over the complex numbers as and thus not absolutely irreducible.
Mathematics is a broad subject that is commonly divided in many areas that may be defined by their objects of study, by the used methods, or by both. For example, analytic number theory is a subarea of number theory devoted to the use of methods of analysis for the study of natural numbers.
Algorithms and Combinatorics is a book series in mathematics, and particularly in combinatorics and the design and analysis of algorithms. It is published by Springer Science+Business Media, and was founded in 1987.
Frances Y. Kuo is an applied mathematician known for her research on low-discrepancy sequences and quasi-Monte Carlo methods for numerical integration and finite element analysis. Originally from Taiwan, she was educated in New Zealand, and works in Australia as a professor in applied mathematics at the University of New South Wales.

Robert Franz Tichy is an Austrian mathematician and professor at Graz University of Technology.
Gerhard Larcher is an Austrian mathematician and professor of financial mathematics at the Johannes Kepler University (JKU) in Linz, Austria. He is the head of the Institute of Financial Mathematics.